Chapter 10: Simple Meter—triplets and sextuplets
About This Chapter
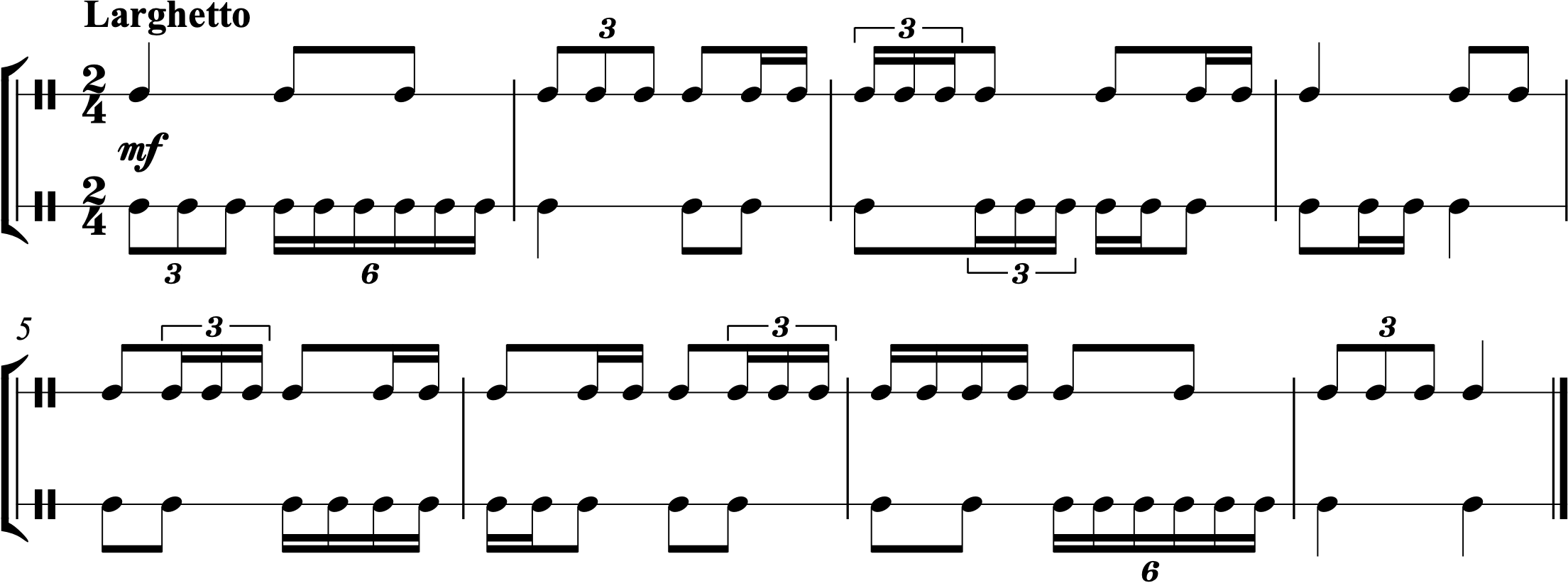
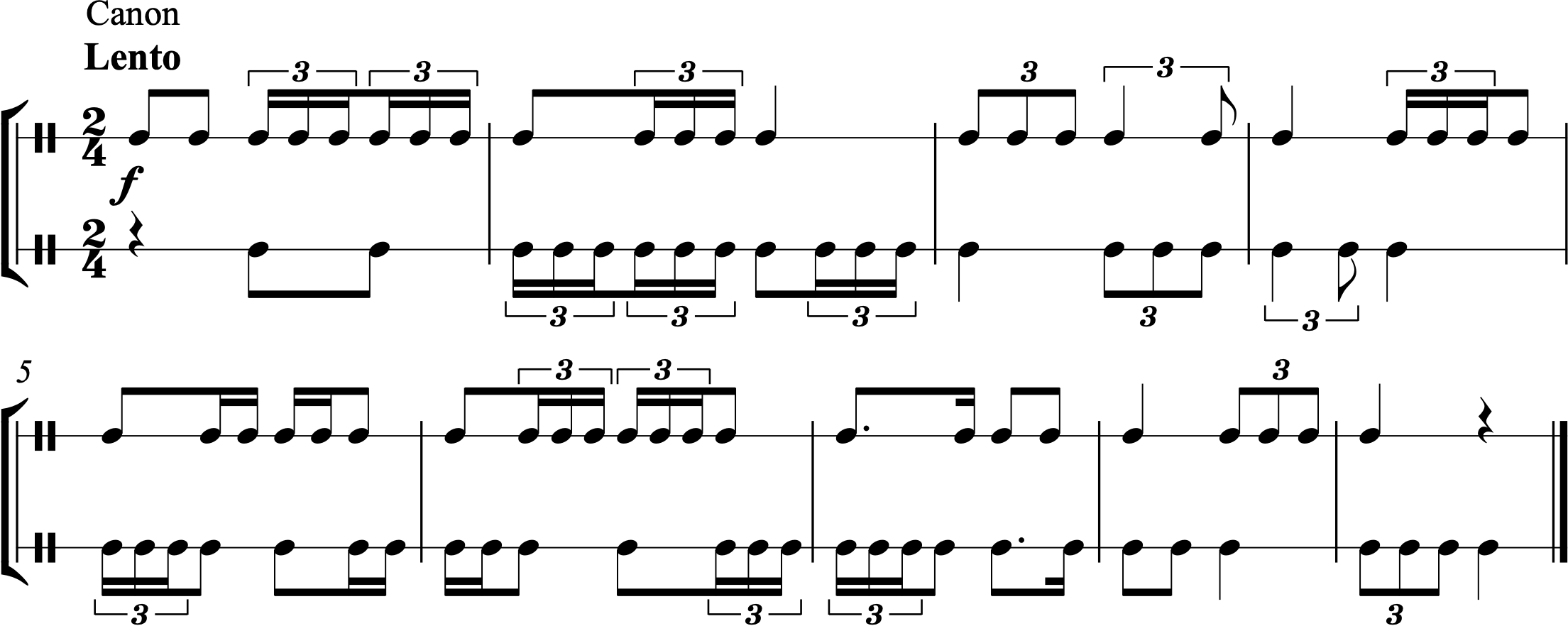
About This Chapter: Up until now, we’ve seen simple meter examples in which the beat divides into two or four parts and compound meter examples in which the beat divides into three or six parts. But sometimes we borrow divisions that don’t fit into the normal metrical grid for the meter we’re in. In this chapter, we’ll explore triplets in simple meter. If we’re in 2/4, the typical division of the beat is into two parts (as shown in measure 1 of the figure below). But sometimes, we’ll see the beat—even though it’s in simple meter—divided into three equal parts like in compound meter! Because we can think of these triplets as borrowed from compound meter’s three-part division of the beat, we’ll borrow the syllables we use in compound meter: “1 la li 2 la li.” These irregular divisions are easy to spot in the score because they include a number (in the case of a triplet, “3”) alongside the beam or in a bracket.
We can also subdivide the beat into six equal parts, just like we do in compound meter. In this case, we’ll show the irregular division with a “6” alongside the beam. In the example below, measure 2 shows us subdividing the triplets in measure 1 in half, creating sextuplets. Once again, we’ll borrow the rhythmic syllables from compound meter: “1 ta la ta li ta.”
The rhythm in measure 4 sounds identical to that in measure 2; however, it is both notated and spoken differently. Measure 4 divides each of the eighth notes of measure 3 into three equal parts—creating sixteenth-note triplets. While we could still speak this as “1 ta la ta li ta,” it may be easier to perform using the syllables “1 la li & la li,” since that accents the “1 &” of the eighth notes that have each been divided into three parts.
Notation: How do you know which note values to use for a triplet or sextuplet? A triplet indicates that we should perform 3 equally spaced notes in the time that 2 would normally go. The normal divisions of simple meter are into 2 parts or 4 parts or 8 parts and so on. But we’re borrowing a division into 3 parts. What we want to do is use the rhythmic value of the closest normal division below this number. So we use the rhythmic value of the division into 2 parts. If we were dividing into five parts (which we’ll do in Chapter 21), we would use the rhythmic value of the division into 4 parts.
Section A—Introduction to eighth-note triplets
Practice
Practice A:
 Practice by performing along with this audio file, which features a metronome click and the notated rhythm. You will hear one measure of wood block to establish the tempo before the exercise begins.
Practice by performing along with this audio file, which features a metronome click and the notated rhythm. You will hear one measure of wood block to establish the tempo before the exercise begins.
Next, try performing along with this audio file, which features the notated rhythm but no metronome click. You will hear one measure of wood block to establish the tempo before the exercise begins.
1.
2.
3.
4.
5.
6.
7
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
Section B—Introduction to sextuplets
Practice
Practice B:
Practice by performing along with this audio file, which features a metronome click and the notated rhythm. You will hear one full measure of wood block to establish the tempo before the exercise begins.
Next, try performing along with this audio file, which features the notated rhythm but no metronome click. You will hear one full measure of wood block to establish the tempo before the exercise begins.
20.
21.
22.
23.
24.
25.
26.
27.
29.
30.
31.
32.
33.
34.
35.
36.
37.
Section C—Two-part rhythms featuring eighth-note triplets and sextuplets
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
Rhythmic Cells
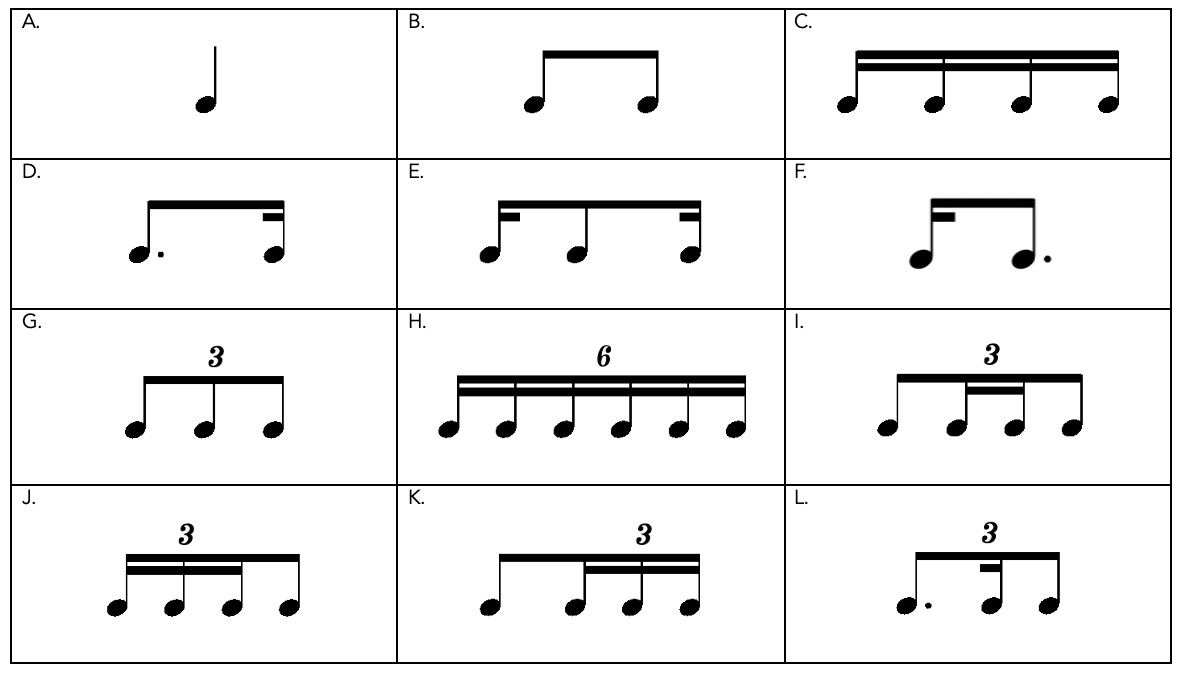
- For general suggestions on how to use these rhythmic cells, see Appendix: How to Use Rhythmic Cells.
- The first two rows feature rhythms that align with the usual divisions of simple meter, while the last two rows feature rhythms that are borrowed from compound meter (division of the beat into three parts instead of two). Experiment with combining simple and compound meter beats.
Rhythm in Context
Rhythm in Context example coming soon!
Citations
Poem:
- Waring Coney (1906–1976), “I Think I See Him There,” public domain. From Caroling Dusk: An Anthology of Verse by Negro Poets, ed. Countee Cullen, published 1927, by Harper & Brothers, New York, NY.
Psalm:
- Scripture taken from the KJV, 1987, public domain.
Rhythm in Context: