5 Lab 5. Mental Imagery: What Can You See in Your “Mind’s Eye?”

COGLAB Exercise 38

Introduction

Mental imagery was a favorite topic of the classic introspectionists. In fact, one of the raging debates around the turn of the century was whether there was such a thing as “imageless thought.” It was widely accepted that most “thoughts” involved images (if you were thinking of an apple, you imagined an apple in your mind). However, some introspectionists held that all thought involved images. The debate was never really settled, as the rise of behaviorism brought an early end to the argument. Mental activity, according to the behaviorists, was not a relevant venue for study.

As the cognitive revolution took hold in the 1960s, the topic of mental imagery again became controversial. Ironically, though, the debate took a different form. Rather than debating whether thinking could occur without images, now the argument was whether or not there was such a thing as mental imagery! Some held that all thought was done verbally, and that there were no mental images.

On the surface, this might seem like an impossible debate. After all, how can we possibly know if there are images? We can’t very well open up somebody’s head and take a look! In the early 1970s, Roger Shepard devised a technique that, in a sense, did allow us to see what is going on with the images inside our heads.

Thought Question:

Try this example: Look at the letters below, and decide whether they are the normal letter, but rotated, or whether they are reversed (backwards) letters:

Do the Thought Question exercise above. You probably had little trouble realizing that the top row is comprised of normal letters, and the bottom row of reversed letters. But did you find that the middle three columns (the ones rotated either 90, 180, or 270 degrees) were somewhat more difficult? Most people do, and require the most time to make a decision when the letters are rotated 180 degrees.

Introspect for a moment: how did you perform the task above? Most people report that they somehow mentally rotate the letters until they are vertical in minds, and then make their judgment. The more the letter is rotated, the longer it will take to rotate it back to the proper position in your mind. Mental rotation exercises such as these have become a favorite way to investigate mental imagery.

The topic of mental imagery is tricky. We know that you don’t have perfect snapshots of objects in your mind. That’s just not the way memory works. How, then, are these mental images stored, and how do we operate upon them? According to Shepard (Shepard & Chipman, 1970; Shepard, 1978; Shepard & Metzler, 1971), images are not perfect copies of real objects, but second-order isomorphisms. This is a fancy term, but all it means is that the image you have is lawfully related to the real object. An isomorphism means that something has the same form (iso-same, morph-form). A first-order isomorphism would be something like a photograph, where the two forms were highly similar (they were related on the “first-order”). A second-order form means that though the mental and physical objects are not identical, they are still similar—perhaps a cartoon rendition of a sunset, rather than an actual video of one. The way we mentally work on the internal object is related to the way we would physically work on the external object. If we have an inverted object in the real world, we physically rotate it. If we have an inverted mental object, we mentally rotate it.

Roger Shepard and his colleagues found evidence to support the concept of second-order isomorphisms in mental rotation. The time required to identify a stimulus was directly related to the stimuli’s “degree of rotation,” similar to the pattern shown in Figure 5.1. This finding has been replicated many times, and also extends into rotations in three dimensions (you may remember those 3-dimensional rotation tests from the standardized achievement tests often given in elementary schools).

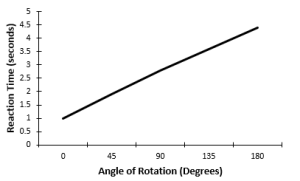
Figure 5.1. A typical relationship between the time required to identify a stimulus and the degree of rotation.

This is not the only way to study mental imagery. For example, Kosslyn, Ball, and Reisser (1978) performed an experiment I refer to as the “Gilligan’s Island” experiment. They had subjects memorize the layout of a fictitious island that had various landmarks. Assume that the island looked like that shown in Figure 5.2.

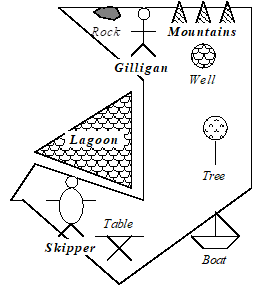
Figure 5.2. A map (vaguely) resembling that memorized by the subjects in Kosslyn, Ball, and Reisser (Kosslyn et al., 1978)

Subjects studied the map for several minutes, memorizing the location of various objects. Then, Kosslyn et al. (1978) asked subjects to imagine they were “at” one location on the island–let’s say, for example, they were told to “go” to the boat in their minds. Once subjects said that they had mentally “located” the boat, they were given the name of a second location–let’s say, the “rock.” They were told to locate the second object as quickly as they could in their mental map of the island, and press a button when they were finished. The question that Kosslyn et al. (1978) were asking is similar to that asked by Shepard and Metzler. Does it take time to scan from one location to another in a mentally imagined environment? Kosslyn et al. (1978) then compared the scanning time for the mental image to the physical distance on the map. The relationship is shown in Figure 5.3.

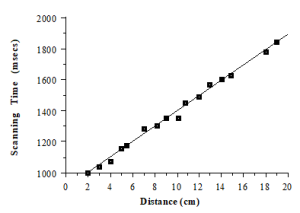
Figure 5.3. Scanning times (milliseconds) as a function of the physical distance between the two points, adapted from Kosslyn et al. (1978)

As you can see, the time to scan the mental image is directly related to the physical distance between the two objects. Do you physically move from one location to the other in your mental map? That may be putting it too strongly; however, the concept of “second-order isomorphisms” allows us to say that while you might not physically move, you are doing something indirectly tied to the literal, physical representation12.

The experiment we are going to perform is similar to one first conducted by Shepard and Metzler (1971). You will be asked to judge whether two images are identical but rotated, or whether they are both rotated and reversed.

At this time, complete the experiment rotation of mental rotation in COGLAB. Instructions can be found in

Lab 38 of the COGLAB Website.

Questions for Lab 5

1. What is the independent variable in these studies? What is the dependent variable?

2. What things were controlled for in the present experiment? Why were they controlled? Can you think of other important variables that we didn’t control? How might we improve the experiment, controlling for those additional factors?

3. Calculate the speed of rotation in degrees per second for both your individual and the class data. How does our figure compare with that of Shepard and Metzler? Why might there be some discrepancies?

4. Why did Shepard & Metzler’s (1971) findings suggest that mental images were similar to real images?

5. In demonstrations like this, participants often report that they mentally rotate the objects in their minds in order to make their same/different judgments, so why did researches decide to take reaction time measurements also?

6. You are trying to get a new mattress through your front door. Currently, the mattress is laying flat on your front porch. You look at the mattress and mentally rotate the object in your mind to figure out how it might fit through the doorway. There are two ways the mattress could conceivably fit through the doorway: it could be slightly tilted to one side or it could be stood up on end. Using what you have learned in this demonstration, which of these two possibilities are you more likely to come up with first? Why?

7. This experiment examined mental imagery. What about imagery for other senses? Give at least two examples of mental representations for other senses, specifically sound and taste/odor.

Data Sheet for Lab 5

Report Mean Percent Reaction time

Speed of Rotation: _______ degrees per second

Graphs for Lab 5

3-D Mental Rotation

Individual Data

NAME:

3-D Mental Rotation

Group Data

NAME: