6 Lab 6. Serial Position Effects

Classroom Demonstration

Introduction

Psychologists can learn a great deal about the structure and functioning of the cognitive system in some very simple ways. You have already seen demonstrations where we infer mental operations because some tasks take longer than others–in reaction time studies, for example. In simple recall studies, we are often more interested in what you forget than what you recall. Why do you forget some things more readily than others?

One of the techniques that has been used for a number of years in the study of memory is a free recall task. In such studies, a subject is given a list of items to be remembered, usually a list of common words. The words are spoken quickly, usually one every second or two. After the experimenter has finished reading the list of words, the subject is asked to recall the words he or she has just heard, in any order. If the list is longer than about 6 or 7 words, some words are inevitably not recalled. What is the source of this pattern of remembering? Are some words, say those in the middle of the list, systematically recalled better or worse than others, or does the forgetting appear to be random? What can we infer about the nature of your memory on the basis of which items are remembered and which are not?

Procedure

You will need three sheets of paper to participate in this experiment. Please bring them to class with you. Mark one of them “List 1,” the second “List 2,” and the third, “List 3.”

You will be read a list of 15 words, presented one every two seconds. Following the reading of this first list, write down all the words you can recall on the first sheet of paper. You will be given three minutes to recall as many words as possible.

The second list will be very similar to the first. However, following the presentation of the second list, you will be given a 3-digit number, like 745. In your mind, subtract 7 from that number over and over again. In other words, if you are given 745, subtract 7, and get 738. Then 738 minus 7 is 731, minus 7 is 724, etc. Keep subtracting for 20 seconds. The experimenter will let you know when the interval is over. When you have finished with the subtraction, write the result in the upper right hand corner of the paper, and then proceed to recall as many words from the list of 15 as you can. Once again, you will be given three minutes to recall as many words as you can.

After you have recalled the second list of 15 items, the experimenter will ask you to write down one more list of items. Those instructions will be given later.

STOP READING AT THIS POINT AND PARTICIPATE IN THE EXPERIMENTS. PLEASE DO NOT READ ANY FURTHER UNTIL THE EXPERIMENTS ARE OVER.

TABLE 6.1. Serial recall performance on List 1.

Total Number of Subjects:

TABLE 6.2. Serial recall performance on List 2.

Total Number of Subjects:______

Table 6.3 Serial Position Recall of Presidents

Total Number of People:

Table 6.3 Serial Position Recall of Presidents (continued)

Theoretical Background

Serial Position Effects in Episodic Memory

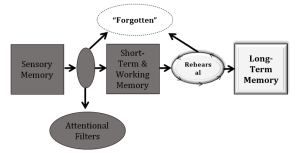
It may seem to you that our everyday notions of Short-Term Memory (STM) and Long-Term Memory (LTM) have always existed. Nothing could be further from the truth. Though the concept of dual memory stores was discussed as far back as the time of William James (1890/1950), it was not until the advent of modern information processing theories that dual-store models of STM and LTM were taken seriously.13 The development of fully-testable models was pioneered by Waugh and Norman (1965) and Atkinson and Shiffrin (Atkinson & Shiffrin, 1968, 1971).

The Atkinson and Shiffrin model of an information processing system postulates three stores:

a) sensory memory, which is very brief in duration and tied strongly to the sensory modality (see Sperling, 1960 and {Crowder, 1969 #5437, for a discussion of sensory stores in vision and audition). The phonological loop and visuo-spatial sketchpad are components of sensory memory.

b) short-term memory, which is limited in capacity to roughly 7 ± 2 items (see the classic Miller paper [1956] on the “Magic Number 7 ± 2”), and is subject to rapid forgetting if the material is not actively rehearsed.

c) long-term memory, which is considered to be a relatively permanent store of information. Furthermore, LTM seems to have an unlimited capacity for storage.

Much of the evidence for the Atkinson and Shiffrin model came from the examination of what are called serial position curves. If you plot the frequency of recalling a given item as a function of position of that item in the list, you find that in most cases, the items at the first of the list are recalled well (this is called a primacy effect), items at the end of the list are recalled well (this is called a recency effect), but items in the middle of the list are recalled with much less consistency. What kind of a memory model could account for such findings?

In the Atkinson and Shiffrin model, information was assumed to come in through the sensory store before being passed on to STM for rehearsal. If the information was rehearsed extensively enough, it was then thought to be passed along from STM into LTM. In the Atkinson and Shiffrin model, the critical prediction was that the probability of recall should be a function of the amount of time that items spent in the rehearsal buffer–namely, how long it spent in STM.

While Atkinson and Shiffrin could not directly observe rehearsal, they could make some pretty good predictions based on which items were probabilistically being rehearsed. It stands to reason that the first item on the list will be rehearsed for a long time. There are no other competing items in the buffer, so rehearsal should be lengthy and uninterrupted. When the second item comes into the buffer, it begins to compete with the first item for space in STM. Despite such competition, STM will likely still have enough room for rehearsal of both items. However, by the time the 4th, 5th, 6th, etc. items start coming into STM, things become crowded, and some items are going to have to be removed from the buffer.

Atkinson and Shiffrin assumed that once the buffer was full, items would start getting removed from the buffer at random. However, the first few items, which were presented alone, got a few extra rehearsal cycles without much competition. Atkinson and Shiffrin reasoned that the first few items in the list should be better recalled because of the extra rehearsal time they had with relatively little competition. This is how they accounted for the primacy effect. Items from the first part of the list are recalled better by almost every subject. Why would this be the case? According to the Atkinson and Shiffrin model, it’s because they had extra rehearsal in STM.

What about the tendency towards increased recall of items at the end of the list (the recency effect)? The Atkinson and Shiffrin model presumed that this was a result of STM functioning. Since this was a free recall paradigm, subjects could reproduce the items in any order they wished. Examination of the output suggested that the first items recalled were often the last ones on the list. Many subjects would report, “Oh, I ‘dumped’ the recent items out of my STM to start with, and then went searching in LTM for the first ones.”

Thus, it seems that what subjects are doing in the free recall task is first mentioning all the items that they have currently stored in STM, and then retrieving items from LTM. Why would the last items present in the list be recalled more frequently? Atkinson and Shiffrin explained the recency effect by postulating that recent items had a high probability of still being in STM.

Atkinson and Shiffrin also reasoned that any task that interfered with STM should remove whatever recency effects might exist. The mental subtraction task prohibited any STM rehearsal of those items. Since STM is very fleeting, even 20 seconds of STM interruption was enough for those items to be lost from STM.

It has long been known that distinctive items are also better remembered. This experiment demonstrated this effect, named the von Restorff effect after its early discoverer (von Restorff, 1933). Because the one item–the word “Batman”– was so different from others, it stood out, and thus was rehearsed considerably more than the other words on the list. You’d see the same effect if a pregnant mother was reading through a list of potential names for her baby, and one of them was “Incrediblehulk.” Or if a counselor was reading you a list of available science classes, and included “Competitive Blackjack Strategy.” That is, so long as the other names were Jim, Bob, etc., and the other classes were biology, chemistry, etc.

Serial Position Effects in Semantic Memory

Just as Atkinson and Shiffrin broke memory down into STM and LTM, others have suggested additional breakdowns of memory. Perhaps the most influential of these memory models was presented by Tulving (Tulving, 1972, 1983; Tulving, 1993). Tulving proposed that your memory system can be broken down into two components: procedural memory and declarative memory; declarative memory can further be broken into episodic memory and semantic memory. Your episodic memories consist of all your “personal” memories, ones in which you are a participant. Your memories of your high school graduation, your memory of your first day on campus, your memory of the time your friend wanted to name her baby Incrediblehulk–these are all personal memories, ones that directly involve you. These are all examples of Tulving’s episodic memories. All of these memories involve personal, discrete episodes–hence their name.

Episodic memory can be contrasted with our warehouse of knowledge, or what we call our semantic memory. This is information that is not tied to any specific learning episode. For example, we all know that President John Kennedy was shot in Dallas in 1963. It is one of the facts that we have in our semantic memory. However, very few of us can probably recall the specific learning episode in which that learning originally took place. Any episodic traces of that memory have been forgotten, but the semantic traces are very much intact. Your semantic memory is vast. Most of what you have learned in school during the last 12 or 14 years is stored in your semantic memory.

The Atkinson and Shiffrin free recall studies dealt with episodic memory. They asked subjects to recall a small group of words that they had learned in a previous learning episode. Virtually all serial position learning involves episodic memories. These are designed to determine how much people remember from a single, specific learning trial. However, several years ago, Roediger and Crowder (1976) discovered what appeared to be a serial position effect for semantic memory. They asked a group of students to recall all the U.S. presidents that they could remember. What they got was a curve that looks remarkably like an episodic serial position curve. Presidents at the early part of our nation’s history were well-remembered (such as Washington and Jefferson), and those in the most recent years were recalled quite frequently (such as LB Johnson and Reagan). Conversely, presidents in the middle (Pierce, Fillmore) were recalled quite poorly, with one notable exception: Lincoln. Roediger and Crowder (1976) explain the high levels of recall concerning Lincoln to be a kind of von Restorff effect. Lincoln is better remembered because he was distinctive.

What kind of conclusions should be drawn from the similarities? It’s difficult to say. It’s certainly possible that any semantic memories that are ordered may show a kind of serial position effect. Few people forget months of the year, but presumably, if they did, they’d forget July before January. It’s certainly hard to remember all the cranial nerves if you don’t recall them in order with the help of a mnemonic device.

The serial curve observed with recall of the presidents may be nothing more than an intriguing coincidence. While it shares the same characteristics of curves depicting episodic memories, it could be the result of radically different causes. Nonetheless, any demonstration of a serial position curve in semantic memory is interesting.

The Roediger and Crowder (1976) article is available in the library (and it is also reprinted in the first edition of Memory Observed). You may find it useful to read the article, and relate what they are saying to the task you performed when you recalled the list of the presidents. Use the article to help you answer the questions for this lab.

Questions for Lab 6

1. Draw serial position curves for Lists 1 & 2. Serial position curves plot percentage recalled as a function of position of the item in the list.

On the curves you draw, label the following:

• the primacy effect
• the recency effect,
• the von Restorff effect (if appropriate).

3. What causes the von Restorff effect? Which list had this effect occur and why? How could you arrange a list, with “Batman” in the same serial position, where it would not show a von Restorff effect?

4. For List 3, draw serial position curves for the free recall criterion. The graph from the Roediger and Crowder (1976) article can serve as a model. Roediger and Crowder also had subjects do positional recall–they had students number their paper from 1 to 40, and then try to recall the presidents in order. What kind of results would you expect to get if we had done this as well?

5. How could the Atkinson and Shiffrin model of memory account for the curves generated with List 3? (Hint: remember that in the Atkinson and Shiffrin model increased rehearsal in STM leads to increased retention in LTM).

6. H.M. wanders into your lab, suffering from permanent anterograde amnesia. He has an intact STM, but no ability to form new LTMs. Draw the shape of the serial position curves that H.M. would likely generate, for both the semantic and episodic lists. Remember that H.M. had his debilitating surgery in 1953.

7. A technology company is holding open interviews from 8am to 2pm this Friday. You are very interested in the job and want to make sure the interviewer remembers you. Using what you have learned in this demonstration, what can you do to make this happen?

Graphs for Lab 6

Serial Position Effects

Group Data Only

Semantic Serial Recall

NAME:

Serial Position Effects

Group Data Only

Episodic Serial Recall

NAME: