4 Lab 4. Searching Short-Term Memory: I Still Haven’t Found What I’m Looking For

COGLAB Exercise 22

Introduction

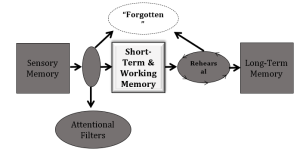
We know that our short-term memory is fleeting–without rehearsal, it lasts no more than 15 seconds or so–and we know from previous research (Miller, 1956)that STM has a small capacity–the “Magic Number 7, plus or minus 2.” How do we search that limited capacity STM buffer? Sternberg (1969) studied this question, and the answers he found might surprise you.

Sternberg’s Methodology

Sternberg’s (1969) experiment, like so many of the truly classic experiments, is elegantly simple. The task was a very simple one for subjects. Sternberg would give them a list of numbers that they would need to remember, called the memory set (or the to-be-remembered set). As an example, he might give them: 3-6-1-8.

Then, he’d give them another number, called the probe digit, and ask the subjects if the probe digit was in the memory set. Subjects simply had to say “yes” or “no.” As you might expect, accuracy was nearly perfect, so Sternberg used reaction time as his primary dependent variable.

Serial or Parallel Search?

The first question Sternberg asked was whether we search the contents of our STM one item at a time (a serial search) or all at once (a parallel search). You use both techniques at times, depending on what it is you’re searching for. Say you are looking for a specific address in your address book, and you only know the person’s first name. You would most likely perform this search by going to the beginning of the address book and looking at each name one at a time. That would be a serial search. But you also search in parallel. Say you are looking for your favorite lime green sweatshirt in the closet. You could search for it by individually going through each piece of clothing. More likely, what you do is scan the whole closet, looking for the distinctive lime green color.10 That would be an example of a parallel search. Which is faster? Without a doubt, the parallel search.

Your long-term memory is usually searched in parallel. The size of your LTM is massive, and a serial search would make efficient retrieval almost impossible. Imagine having to go through the entire contents of your LTM every time you tried to remember your phone number.

Since a parallel search is more efficient, it seems likely that we’d search our STM in parallel. As we said, though, sometimes things are hidden from consciousness, and our introspective intuitions can be wrong.

Sternberg used his memory set/probe digit methodology to answer this question. He reasoned that if we search our STM in parallel, the size of the memory set should be irrelevant. Therefore, in order to determine if the search was serial, Sternberg varied the size of the memory set.

For the sake of clarity, let’s assume the probe digit was always the last digit in the memory set, like this:

Sternberg compared the time it took to verify probe digits in memory sets of sizes 1-5. If the search was parallel, the search times should all be the same: the subject is only searching one thing. If, however, the search is serial, the reaction time should increase linearly with increasing set sizes. Only one item would have to be searched if the set size was one, but five items would need to be searched if the set size was five. The competing predictions are shown in Figure 4.1.

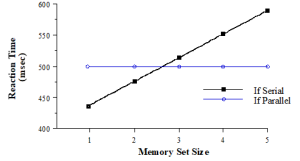
Figure 4.1. Predicted Search times for Serial and Parallel STM Searches

When Sternberg ran this experiment, he found that STM was searched serially. Reaction time increased linearly as memory set size increased. In fact, he found an almost perfect line conforming to the equation:

RT = 400 msec + (38 msec * size of memory set)

In other words, he found that it took subjects 400 msec just to respond (that’s about how long it would take just to press a button when a light flashed on), and then it took them an additional 38 milliseconds to search each additional item.

Exhaustive or Self-Terminating?

Given that Sternberg found that we search STM serially, he next turned his attention to the question of how we terminate our search. Do we stop when we find what we are looking for (called a self-terminating search), or do we continue through the entire list anyway (called and exhaustive search)? The answer appears obvious: Surely we don’t keep looking after we have found the item we were looking for, do we?!? Long-term memory search is clearly self-terminating. If we are hunting for the name of John Adams’ wife, we quit when we find the right answer. In everyday life, we terminate our searches as well. If we are looking for our keys, we quit looking once we have found them. Does short-term memory search follow the same principles?

There are two ways to answer this question. One would be to hold set sizes constant, and vary the position of the probe in the memory set. For example, take the following lists:

Each memory set is of size 4, but for the first list, the probe digit is the first item in the set. For the second list, the probe is the second item in the set, and so on. If our search is terminating, we should see faster times for those lists where the probe digit is early in the set. If, by contrast, the search is exhaustive, we should find the same search time for all 4 lists. Since all lists are of size 4, all should produce the same search times. A graph of the hypotheses appears in Figure 4.2.

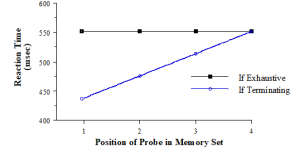
Figure 4.2. Predicted Results for Terminating and Exhaustive Search of STM

A second way to determine whether the search is terminating or exhaustive is to compare positive probes (probes that are in the memory set) with negative probes (probes that are not in the memory set). By definition, the entire list will have to be searched if the probe is negative: you can’t know that something is not in the set until you’ve searched every item in that set. On the other hand, with positive probes, you don’t always have to search the entire set. Say you have a memory set size of 4, and the probe is in the set. One quarter of the time, when the probe digit is in the 4th position in the set, you’ll have to search the entire set (say, if you were searching the set 5-2-8-3 for the probe digit 3). But most of the time you won’t have to search the entire list–you’ll find the probe digit before you come to the end of the list. Specifically, a terminating search predicts that as memory set size increases, reaction times for positive probes will increase only half as fast as for negative probes. In other words, if the probe digit can be in any position in the set, its average position will be in the middle of the set (whether it’s 3 for a 5-digit set, or 5 for a 9-digit set). Negative probes would require you to search the whole list, and would on average take twice as long as positive searches. The competing predictions appear in Figure 4.3. This second way of testing for serial vs. self-terminating searches is the way we will use in this lab.

When Sternberg compared reaction times for positive probes and negative probes, he found that the slopes of the two lines were identical, evidence suggesting that STM search is exhaustive, not terminating. Both lines increased at the rate of 38 milliseconds for each additional item in the memory set. Counter to our intuitions once again, we continue to search the entire contents of STM, even after we have found what we are looking for.

Figure 4.3. Predicted results for Search Times of Positive and Negative Probes, assuming a terminating search.

Summary of Sternberg’s Findings

Initially, before we looked at the data, most of us probably expected STM search to be parallel and not serial, much like our LTM searches. Certainly, most of us anticipated that our search would be terminating rather than exhaustive. It doesn’t make sense to keep searching once we found what it is we’re searching for, does it?

In some ways, it does. An exhaustive search of STM hinges on two factors. First, the size of STM is really quite small. Remember from previous work that STM capacity is usually no more than 7 items, give or take a few. That means the entire contents of our STM can be searched in just over 1/4 of a second (7 items times 38 msec/item). That’s pretty fast.

Second, if we didn’t search the entire contents, we’d have to check the outcome of our search after each comparison. We’d compare the probe digit with the first item in the memory set, and then check the outcome. If they match, we can stop. If they don’t match, we have to go on. Each digit would require not only the comparison of the probe to each digit in the set, but also a checking stage after each comparison, to see if the search can be stopped. Each of those checks takes time.

The way we actually search involves only a single check, after the entire memory set has been searched. It’s true that an exhaustive search is less efficient on those few cases where the probe is one of the first items in the set. But apparently the “search and check, search and check, etc.” approach is less efficient than a “search, search, search…one check” approach11.

At this time, complete the experiment Sternberg Search in COGLAB. Instructions can be found in Lab 22 of the COGLAB Website.

Questions for Lab 4

1. What is the dependent variable in these experiments? What is the independent variable?

2. What important factors were controlled in this experiment? Were there any factors that were missed?

3. On the graphs of both your individual and class data, draw a line of best fit for each graph and compute the slope and intercept of those lines.

• What do the numbers for the slope and intercept mean? That is, what do they represent?
• How do the slope and intercept that you calculated compare to Sternberg’s results?
• If there are large differences between our results and Sternberg’s results, why do you think they are there?

4. If the search had been self-terminating (which it is not!) what would the predicted equation for the positive probes have been? (hint: the equation for negative probes was RT = 400 msec + (38 msec/item * # items). Re-read the section in your lab manual to see the rate of scanning predicted for positive probes)

5. Compute the ratio of the slopes of the positive probes and the negative probes:

RATIO = SLOPE (Positive Probe) / SLOPE (Negative Probes)

According to Sternberg’s work, what should it be? How does our number compare? What should it have been if the search were terminating rather than exhaustive?

6. Do you think it is to our advantage that we use an exhaustive search of short-term memory as opposed to a self-terminating search? Why or why not?

Data Sheet for Lab 4

Name:

Report Mean Correct Reaction Time:

Slopes of the functions relating correct mean reaction time and memory set size:

Positive Probes: Negative Probes:

Intercepts of the functions relating correct mean reaction time and memory set size:

Positive Probes: Negative Probes:

Graphs for Lab 4

Scanning Short Term Memory

Individual Data

NAME:

Scanning Short Term Memory

Group Data

NAME: