Solving Exponential Equations
This content comes directly from OpenStax's textbook Algebra and Trigonometry Section 6.6 Solve Rational Equations
Let's Start by Using Like Bases to Solve Exponential Equations
The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers[latex]\,b,[/latex] [latex]S,[/latex] and[latex]\,T,[/latex] where[latex]\,b>0,\text{ }b\ne 1,[/latex][latex]{b}^{S}={b}^{T}\,[/latex]if and only if[latex]\,S=T.[/latex]
In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.
For example, consider the equation[latex]\,{3}^{4x-7}=\frac{{3}^{2x}}{3}.\,[/latex]To solve for[latex]\,x,[/latex] we use the division property of exponents to rewrite the right side so that both sides have the common base,[latex]\,3.\,[/latex]Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for[latex]\,x:[/latex]
[latex]\begin{array}{cccc}\,\,{3}^{4x-7}\hfill & =& \frac{{3}^{2x}}{3}\hfill & \hfill \\ \,\,{3}^{4x-7}\hfill & =& \frac{{3}^{2x}}{{3}^{1}}\hfill & {\text{Rewrite 3 as 3}}^{1}.\hfill \\ \,\,{3}^{4x-7}\hfill & = & {3}^{2x-1}\hfill & \text{Use the division property of exponents}\text{.}\hfill \\ 4x-7\hfill & =& 2x-1\,\,\text{ }\hfill & \text{Apply the one-to-one property of exponents}\text{.}\hfill \\ \,\,\,\,\,2x\hfill & =& 6\hfill & \text{Subtract 2}x\text{ and add 7 to both sides}\text{.}\hfill \\ \,\,\,\,\,\,\,x\hfill & =& 3\hfill & \text{Divide by 3}\text{.}\hfill \end{array}[/latex]
Using the One-to-One Property of Exponential Functions to Solve Exponential Equations
For any algebraic expressions[latex]\,S\text{ and }T,[/latex] and any positive real number[latex]\,b\ne 1,[/latex]
[latex]{b}^{S}={b}^{T}\,\,\text{if and only if}\,\,S=T[/latex].
How To
Given an exponential equation with the form[latex]\,{b}^{S}={b}^{T},[/latex] where [latex]\,S\,[/latex] and [latex]\,T\,[/latex] are algebraic expressions with an unknown, solve for the unknown.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form[latex]\,{b}^{S}={b}^{T}.[/latex]
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation,[latex]\,S=T,[/latex] for the unknown.
EXAMPLE 15
Solving an Exponential Equation with a Common Base
Solve[latex]\,{2}^{x-1}={2}^{2x-4}.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc} {2}^{x-1} & = & {2}^{2x-4} \hfill & \text{The common base is }2.\hfill \\ \text{ }x-1 & = & 2x-4 \begin{array}{cccc}& & & \end{array}\hfill & \text{By the one-to-one property the exponents must be equal}.\hfill \\ \text{ }\,\,x & = & 3\hfill & \text{Solve for }x.\hfill \end{array}[/latex]
 Try It #7
Try It #7
Solve[latex]\,{5}^{2x}={5}^{3x+2}.[/latex]
Rewriting Equations So All Powers Have the Same Base
Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.
For example, consider the equation[latex]\,256={4}^{x-5}.\,[/latex]We can rewrite both sides of this equation as a power of[latex]\,2.\,[/latex]Then we apply the rules of exponents, along with the one-to-one property, to solve for[latex]\,x:[/latex]
[latex]\begin{array}{ll}256={4}^{x-5}\hfill & \hfill \\ \,\,\,{2}^{8}={\left({2}^{2}\right)}^{x-5}\hfill & \text{Rewrite each side as a power with base 2}.\hfill \\ \,\,\,{2}^{8}={2}^{2x-10}\hfill & \text{Use the one-to-one property of exponents}.\hfill \\ \,\,\,\,\,\,8=2x-10\begin{array}{cccc}& & & \end{array}\hfill & \text{Apply the one-to-one property of exponents}.\hfill \\ \,\,\,18=2x\hfill & \text{Add 10 to both sides}.\hfill \\ \,\,\,\,\,\,x=9\hfill & \text{Divide by 2}.\hfill \end{array}[/latex]
How To
Given an exponential equation with unlike bases, use the one-to-one property to solve it.
- Rewrite each side in the equation as a power with a common base.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form[latex]\,{b}^{S}={b}^{T}.[/latex]
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation,[latex]\,S=T,[/latex] for the unknown.
EXAMPLE 16
Solving Equations by Rewriting Them to Have a Common Base
Solve[latex]\,{8}^{x+2}={16}^{x+1}.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}\,\text{ }{8}^{x+2} & = & {16}^{x+1}\hfill & \hfill \\ {\left({2}^{3}\right)}^{x+2} & = & {\left({2}^{4}\right)}^{x+1}\hfill & \text{Write }8\text{ and }16\text{ as powers of }2.\hfill \\ \text{ }{2}^{3x+6} & = & {2}^{4x+4}\hfill & \text{To take a power of a power, multiply exponents}.\hfill \\ \text{ }3x+6 & = & 4x+4\hfill & \text{Use the one-to-one property to set the exponents equal}.\hfill \\ \,\text{ }x & = & 2\hfill & \text{Solve for }x.\hfill \end{array}[/latex]
 Try It #8
Try It #8
Solve[latex]\,{5}^{2x}={25}^{3x+2}.[/latex]
EXAMPLE 17
Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base
Solve[latex]\,{2}^{5x}=\sqrt{2}.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}{2}^{5x} & = & {2}^{\frac{1}{2}\,\,\,\,\,}\hfill & \text{Write the square root of 2 as a power of }2.\hfill \\ \,\,5x &= &\frac{1}{2}\hfill & \text{Use the one-to-one property}.\hfill \\ \,\,\,\,\,x&= &\frac{1}{10}\hfill & \text{Solve for }x.\hfill \end{array}[/latex]
 Try It #9
Try It #9
Solve[latex]\,{5}^{x}=\sqrt{5}.[/latex]
 Q&A
Q&A
Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem-solving process?
No. Recall that the range of an exponential function is always positive. While solving the equation, we may obtain an expression that is undefined.
EXAMPLE 18
Solving an Equation with Positive and Negative Powers
Solve[latex]\,{3}^{x+1}=-2.[/latex]
Show/Hide Solution
 Solution
Solution
This equation has no solution. There is no real value of[latex]\,x\,[/latex]that will make the equation a true statement because any power of a positive number is positive.
 Analysis
Analysis
Figure 1 shows that the two graphs do not cross so the left side is never equal to the right side. Thus the equation has no solution.
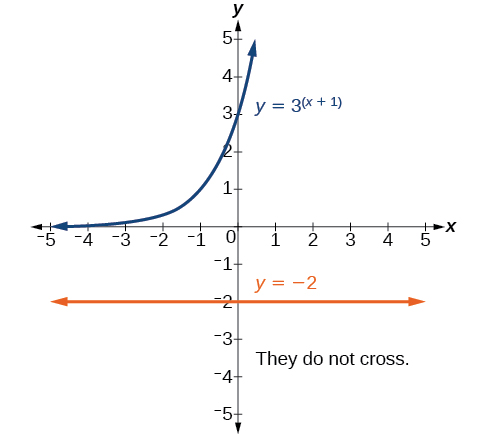
Figure 1
 Try It #10
Try It #10
Solve[latex]\,{2}^{x}=-100.[/latex]
Solving Exponential Equations Using Logarithms
Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since[latex]\,\mathrm{log}\left(a\right)=\mathrm{log}\left(b\right)\,[/latex]is equivalent to[latex]\,a=b,[/latex] we may apply logarithms with the same base on both sides of an exponential equation.
How To
Given an exponential equation in which a common base cannot be found, solve for the unknown.
- Apply the logarithm of both sides of the equation.
- If one of the terms in the equation has base 10, use the common logarithm.
- If none of the terms in the equation has base 10, use the natural logarithm.
- Use the rules of logarithms to solve for the unknown.
EXAMPLE 19
Solving an Equation Containing Powers of Different Bases
Solve[latex]\,{5}^{x+2}={4}^{x}.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}\text{ }\,\,{5}^{x+2} &= & {4}^{x}\hfill & \text{There is no easy way to get the powers to have the same base}.\hfill \\ \text{ }\,\mathrm{ln}{5}^{x+2} & =& \mathrm{ln}{4}^{x}\hfill & \text{Take ln of both sides}.\hfill \\ \text{ }\,\left(x+2\right)\mathrm{ln}5 & = & x\mathrm{ln}4\hfill & \text{Use laws of logs}.\hfill \\ \text{ }x\mathrm{ln}5+2\mathrm{ln}5 & = & x\mathrm{ln}4\hfill & \text{Use the distributive law}.\hfill \\ \text{ }x\mathrm{ln}5-x\mathrm{ln}4 & = & -2\mathrm{ln}5\hfill & \text{Get terms containing }x\text{ on one side, terms without }x\text{ on the other}.\hfill \\ \,\,x\left(\mathrm{ln}5-\mathrm{ln}4\right) & = & -2\mathrm{ln}5\hfill & \text{On the left hand side, factor out an }x.\hfill \\ \text{ }\,x\mathrm{ln}\left(\frac{5}{4}\right) & = & \mathrm{ln}\left(\frac{1}{25}\right)\begin{array}{cccc}& & & \end{array}\hfill & \text{Use the laws of logs}.\hfill \\ \text{ }\,x & = & \frac{\mathrm{ln}\left(\frac{1}{25}\right)}{\mathrm{ln}\left(\frac{5}{4}\right)}\hfill & \text{Divide by the coefficient of }x.\hfill \end{array}[/latex]
 Try It #11
Try It #11
Solve[latex]\,{2}^{x}={3}^{x+1}.[/latex]
 Q&A
Q&A
Is there any way to solve[latex]\,{2}^{x}={3}^{x}?[/latex]
Yes. The solution is [latex]0.[/latex]
Equations Containing e
One common type of exponential equations are those with base[latex]\,e.\,[/latex]This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base[latex]\,e\,[/latex]on either side, we can use the natural logarithm to solve it.
How To
Given an equation of the form[latex]\,y=A{e}^{kt}\text{,}[/latex] solve for[latex]\,t.[/latex]
- Divide both sides of the equation by[latex]\,A.[/latex]
- Apply the natural logarithm of both sides of the equation.
- Divide both sides of the equation by[latex]\,k.[/latex]
EXAMPLE 20
Solve an Equation of the Form y = Aekt
Solve[latex]\,100=20{e}^{2t}.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}100\hfill & = & 20{e}^{2t}\hfill & \hfill \\ \,\,\,5\hfill & = & {e}^{2t}\hfill & \text{Divide by the coefficient of the power}\text{.}\hfill \\ \mathrm{ln}5\hfill & = & 2t\hfill & \text{Take ln of both sides}\text{. Use the fact that }\mathrm{ln}\left(x\right)\text{ and }{e}^{x}\text{ are inverse functions}\text{.}\hfill \\ \,\,\,t\hfill & = & \frac{\mathrm{ln}5}{2}\,\,\,\,\,\hfill & \text{Divide by the coefficient of }t\text{.}\hfill \end{array}[/latex]
 Analysis
Analysis
Using laws of logs, we can also write this answer in the form[latex]\,t=\mathrm{ln}\sqrt{5}.[/latex]If we want a decimal approximation of the answer, we use a calculator.
 Try It #12
Try It #12
Solve[latex]\,3{e}^{0.5t}=11.[/latex]
 Q&A
Q&A
Does every equation of the form[latex]\,y=A{e}^{kt}\,[/latex]have a solution?
No. There is a solution when[latex]\,k\ne 0,[/latex]and when[latex]\,y\,[/latex]and[latex]\,A\,[/latex]are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is[latex]\,2=-3{e}^{t}.[/latex]
EXAMPLE 21
Solving an Equation That Can Be Simplified to the Form y = Aekt
Solve[latex]\,4{e}^{2x}+5=12.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{ll}4{e}^{2x}+5=12\hfill & \hfill \\ \,\,\,\,\,\,\,\,\,\,4{e}^{2x}=7\hfill & \text{Combine like terms}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,{e}^{2x}=\frac{7}{4}\hfill & \text{Divide by the coefficient of the power}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x=\mathrm{ln}\left(\frac{7}{4}\right)\hfill & \text{Take ln of both sides}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{1}{2}\mathrm{ln}\left(\frac{7}{4}\right)\hfill & \text{Solve for }x.\hfill \end{array}[/latex]
 Try It #13
Try It #13
Solve[latex]\,3+{e}^{2t}=7{e}^{2t}.[/latex]
Extraneous Solutions
Sometimes the methods used to solve an equation introduce an extraneous solution, which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.
EXAMPLE 22
Solving Exponential Functions in Quadratic Form
Solve[latex]\,{e}^{2x}-{e}^{x}=56.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}\,\,\,\,\,\,\,\,\,\,\,\,\,{e}^{2x}-{e}^{x}\hfill & = & 56\hfill & \hfill \\ \,\,\,\,{e}^{2x}-{e}^{x}-56\hfill & = & 0\hfill & \text{Get one side of the equation equal to zero}.\hfill \\ \left({e}^{x}+7\right)\left({e}^{x}-8\right)\hfill & = & 0\hfill & \text{Factor by the FOIL method}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{e}^{x}+7\hfill & = & 0\text{ or }{e}^{x}-8=0\begin{array}{cccc}& & & \end{array}\hfill & \text{If a product is zero, then one factor must be zero}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{e}^{x}\hfill & = & -7{\text{ or e}}^{x}=8\hfill & \text{Isolate the exponentials}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{e}^{x}\hfill & = & 8\hfill & \text{Reject the equation in which the power equals a negative number}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\hfill & = & \mathrm{ln}8\hfill & \text{Solve the equation in which the power equals a positive number}.\hfill \end{array}[/latex]
 Analysis
Analysis
When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation[latex]\,{e}^{x}=-7\,[/latex]because a positive number never equals a negative number. The solution [latex]\,\mathrm{ln}\left(-7\right)\,[/latex]is not a real number, and in the real number system this solution is rejected as an extraneous solution.
 Try It #14
Try It #14
Solve[latex]\,{e}^{2x}={e}^{x}+2.[/latex]
 Q&A
Q&A
Does every logarithmic equation have a solution?
No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.
Solving Logarithmic Equations
Let's Start by Using the Definition of a Logarithm to Solve Logarithmic Equations
We have already seen that every logarithmic equation[latex]\,{\mathrm{log}}_{b}\left(x\right)=y\,[/latex]is equivalent to the exponential equation[latex]\,{b}^{y}=x.\,[/latex]We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation[latex]\,{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x-5\right)=3.\,[/latex]To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for[latex]\,x:[/latex]
[latex]\begin{array}{cccc}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x-5\right) & = & 3\hfill & \hfill \\ \text{ }\,{\mathrm{log}}_{2}\left(2\left(3x-5\right)\right) & = & 3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x-10\right) & = & 3\hfill & \text{Distribute}.\hfill \\ \text{ }\,\,{2}^{3} & = & 6x-10\hfill & \text{Apply the definition of a logarithm}.\hfill \\ \text{ }8 & = & 6x-10\begin{array}{cccc}& & & \end{array}\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18 & = & 6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }\,x & = & 3\hfill & \text{Divide by 6}.\hfill \end{array}[/latex]
Using the Definition of a Logarithm to Solve Logarithmic Equations
For any algebraic expression[latex]\,S\,[/latex]and real numbers[latex]\,b\,[/latex]and[latex]\,c,[/latex]where[latex]\,b>0,\text{ }b\ne 1,[/latex]
[latex]{\mathrm{log}}_{b}\left(S\right)=c\,\,\text{if and only if}\,\,{b}^{c}=S[/latex]
EXAMPLE 23
Using Algebra to Solve a Logarithmic Equation
Solve[latex]\,2\mathrm{ln}x+3=7.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}2\mathrm{ln}x+3 & = & 7\hfill & \hfill \\ \text{ }\,\,2\mathrm{ln}x & = & 4\hfill & \text{Subtract 3}.\hfill \\ \text{ }\,\,\mathrm{ln}x & = & 2\hfill & \text{Divide by 2}.\hfill \\ \text{ }\,x & = & {e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{array}[/latex]
 Try It #15
Try It #15
Solve[latex]\,6+\mathrm{ln}x=10.[/latex]
EXAMPLE 24
Using Algebra Before and After Using the Definition of the Natural Logarithm
Solve[latex]\,2\mathrm{ln}\left(6x\right)=7.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccc}2\mathrm{ln}\left(6x\right) & = & 7\hfill & \hfill \\ \text{ }\mathrm{ln}\left(6x\right) & = & \frac{7}{2}\hfill & \text{Divide by 2}.\hfill \\ \text{ }6x & = & {e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{ }x & = & \frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide by 6}.\hfill \end{array}[/latex]
 Try It #16
Try It #16
Solve[latex]\,2\mathrm{ln}\left(x+1\right)=10.[/latex]
EXAMPLE 25
Using a Graph to Understand the Solution to a Logarithmic Equation
Solve[latex]\,\mathrm{ln}x=3.[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{ll}\mathrm{ln}x=3\hfill & \hfill \\ \,\,\,\,\,x={e}^{3}\hfill & \text{Use the definition of the natural logarithm}\text{.}\hfill \end{array}[/latex]
Figure 2 represents the graph of the equation. On the graph, the x-coordinate of the point at which the two graphs intersect is close to 20. In other words[latex]\,{e}^{3}\approx 20.\,[/latex]A calculator gives a better approximation:[latex]\,{e}^{3}\approx 20.0855.[/latex]
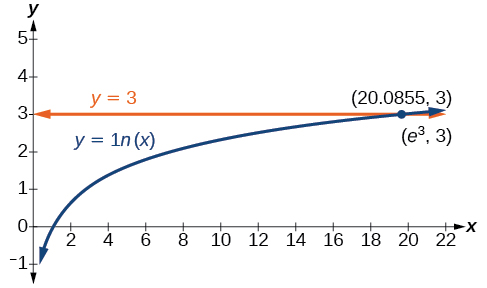
Figure 2
 Try It #17
Try It #17
Use a graphing calculator to estimate the approximate solution to the logarithmic equation[latex]\,{2}^{x}=1000\,[/latex]to 2 decimal places.
Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers[latex]\,x>0,[/latex] [latex]S>0,[/latex] [latex]T>0\,[/latex]and any positive real number[latex]\,b,[/latex] where[latex]\,b\ne 1,[/latex]
[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T.[/latex]
For example,
[latex]\text{If }{\mathrm{log}}_{2}\left(x-1\right)={\mathrm{log}}_{2}\left(8\right),\text{then }x-1=8.[/latex]
So, if[latex]\,x-1=8,[/latex]then we can solve for[latex]\,x,[/latex]and we get[latex]\,x=9.\,[/latex]To check, we can substitute[latex]\,x=9\,[/latex]into the original equation:[latex]\,{\mathrm{log}}_{2}\left(9-1\right)={\mathrm{log}}_{2}\left(8\right)=3.\,[/latex]In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
For example, consider the equation[latex]\,\mathrm{log}\left(3x-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right).\,[/latex]To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for[latex]\,x:[/latex]
[latex]\begin{array}{cccc}\mathrm{log}\left(3x-2\right)-\mathrm{log}\left(2\right) & = & \mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{ }\,\,\,\mathrm{log}\left(\frac{3x-2}{2}\right) & = & \mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{ }\,\,\frac{3x-2}{2} & = & x+4\hfill & \text{Apply the one to one property of a logarithm}.\hfill \\ \text{ }\,\,\,3x-2 & = & 2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{ }\,\,x & = & 10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}[/latex]
To check the result, substitute[latex]\,x=10\,[/latex]into[latex]\,\mathrm{log}\left(3x-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right).[/latex]
[latex]\begin{array}{cccc}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right) & = & \mathrm{log}\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{ }\,\mathrm{log}\left(28\right)-\mathrm{log}\left(2\right) & = & \mathrm{log}\left(14\right)\hfill & \hfill \\ \text{ }\,\,\mathrm{log}\left(\frac{28}{2}\right) & = & \mathrm{log}\left(14\right)\hfill & \text{The solution checks}.\hfill \end{array}[/latex]
Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
For any algebraic expressions[latex]\,S\,[/latex]and[latex]\,T\,[/latex]and any positive real number[latex]\,b,[/latex] where[latex]\,b\ne 1,[/latex]
[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\,\,\text{if and only if}\,\,S=T[/latex]
Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.
How To
Given an equation containing logarithms, solve it using the one-to-one property.
- Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form[latex]\,{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T.[/latex]
- Use the one-to-one property to set the arguments equal.
- Solve the resulting equation,[latex]\,S=T,[/latex] for the unknown.
EXAMPLE 26
Solving an Equation Using the One-to-One Property of Logarithms
Solve[latex]\,\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right).[/latex]
Show/Hide Solution
 Solution
Solution
[latex]\begin{array}{cccccccc} & & \text{ }\,\,\,\,\,\,\,\,\mathrm{ln}\left({x}^{2}\right) & = & \mathrm{ln}\left(2x+3\right)\hfill & & & \hfill \\ & & \text{ }\,\,\,\,\,\,{x}^{2} & = & 2x+3\hfill & & & \text{Use the one-to-one property of the logarithm}.\hfill \\ & & \text{ }\,\,\,{x}^{2}-2x-3 & = & 0\hfill & & & \text{Get zero on one side before factoring}.\hfill \\ & & \,\,\,\left(x-3\right)\left(x+1\right) & = & 0\hfill & & & \text{Factor using FOIL}.\hfill \\ \hfill x-3 & = & 0 \hfill & \hfill \text{or}\hfill & \hfill x+1 & = & 0 \hfill & \text{If a product is zero, one of the factors must be zero}. \hfill \\ \hfill x & = & 3 \hfill & \hfill \text{or} \hfill & \hfill x & = & -1 \hfill & \text{Solve for }x. \hfill \end{array}[/latex]
 Analysis
Analysis
There are two solutions: [latex]\,3\,[/latex] or [latex]\,-1.\,[/latex]The solution [latex]\,-1\,[/latex]is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.
 Try It #18
Try It #18
Solve[latex]\,\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(1\right).[/latex]
Section 3.1 Exercises
[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]
Factor each of the following quadratics completely.
1. [latex]7{x}^{2}-19x-6[/latex]
2. [latex]3{n}^{2}-2n-8[/latex]
3. [latex]7{b}^{2}+15b+2[/latex]
4. [latex]21{v}^{2}-11v-2[/latex]
5. [latex]5{a}^2+13a-6[/latex]
6. [latex]5{n}^{2}-18n-8[/latex]
7. [latex]2{x}^{2}-5x+2[/latex]
8. [latex]3{r}^{2}-4r-4[/latex]
9. [latex]2{x}^{2}+19x+35[/latex]
10. [latex]3{x}^{2}+4x-15[/latex]
11. [latex]2{b}^{2}-b-3[/latex]
12. [latex]2{k}^{2}+5k-12[/latex]
13. [latex]4{k}^{2}-17k+4[/latex]
14. [latex]4{r}^2+3r-7[/latex]
15. [latex]5{n}^{2}+21n+4[/latex]
16. [latex]8{w}^{2}+25w+3[/latex]
17. [latex]9{z}^{2}+15z+4[/latex]
18. [latex]3{m}^{2}+26m+48[/latex]
19. [latex]4{k}^{2}−16k+15[/latex]
20. [latex]4{q}^{2}−9q+5[/latex]
21. [latex]5{s}^{2}−9s+4[/latex]
22. [latex]4{r}^{2}−20r+25[/latex]
23. [latex]6{y}^{2}+y−15[/latex]
24. [latex]6{p}^{2}+p−22[/latex]
25. [latex]2{n}^{2}−27n−45[/latex]
26. [latex]12{z}^{2}−41z−11[/latex]
27. [latex]3{x}^{2}+8x+4[/latex]
28. [latex]4{y}^{2}+15y+6[/latex]
29. [latex]60{y}^{2}+290y−50[/latex]
30. [latex]6{u}^{2}−46u−16[/latex]
31. [latex]48{z}^{3}−102{z}^{2}−45z[/latex]
32. [latex]90{n}^{3}+42{n}^{2}−216n[/latex]
33. [latex]16{s}^{2}+40s+24[/latex]
34. [latex]24{p}^{2}+160p+96[/latex]
35. [latex]48{y}^{2}+12y−36[/latex]
36. [latex]30{x}^{2}+105x−60[/latex]
In the following exercises, solve by using the Quadratic Formula.
37. [latex]2{a}^{2}−6a+3=0[/latex]
38. [latex]5{b}^{2}+2b−4=0[/latex]
39. [latex]2{x}^{2}+3x+9=0[/latex]
40. [latex]6{y}^{2}−5y+2=0[/latex]
41. [latex]2{a}^{2}+12a+5=0[/latex]
42. [latex]4{d}^{2}−7d+2=0[/latex]
Solve each of the following.
43. [latex]1+\frac{9}{p}=−\frac{20}{{p}^{2}}[/latex]
44. [latex]\frac{5}{y−9}+\frac{1}{y+9}=\frac{18}{{y}^{2}−81}[/latex]
45. [latex]\frac{8}{z−10}+\frac{7}{z+10}=\frac{5}{{z}^{2}−100}[/latex]
46. [latex]\frac{w+8}{{w}^{2}−11w+28}=\frac{5}{w−7}+\frac{2}{w−4}[/latex]
47. [latex]\frac{x−10}{{x}^{2}+8x+12}=\frac{3}{x+2}+\frac{4}{x+6}[/latex]
48. [latex]\frac{m}{m+5}=\frac{50}{{m}^{2}−25}+6[/latex]
49. [latex]\frac{d}{d+3}=\frac{18}{{d}^{2}−9}+4[/latex]
50. [latex]\frac{r}{3r−15}−\frac{1}{4r+20}=\frac{3{r}^{2}+17r+40}{12{r}^{2}−300}[/latex]
51. [latex]\frac{s}{2s+6}−\frac{2}{5s+5}=\frac{5{s}^{2}−s−18}{10{s}^{2}+40s+30}[/latex]
52. [latex]\frac{t}{6t−12}−\frac{5}{2t+10}=\frac{{t}^{2}−23t+70}{12{t}^{2}+36t−120}[/latex]
Verbal
53. How can an exponential equation be solved?
54. When does an extraneous solution occur? How can an extraneous solution be recognized?
55. When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?
Algebraic
For the following exercises, use like bases to solve the exponential equation.
56. [latex]{4}^{-3v-2}={4}^{-v}[/latex]
57. [latex]64\cdot {4}^{3x}=16[/latex]
58. [latex]{3}^{2x+1}\cdot {3}^{x}=243[/latex]
59. [latex]{2}^{-3n}\cdot \frac{1}{4}={2}^{n+2}[/latex]
60. [latex]625\cdot {5}^{3x+3}=125[/latex]
61. [latex]\frac{{36}^{3b}}{{36}^{2b}}={216}^{2-b}[/latex]
62. [latex]{\left(\frac{1}{64}\right)}^{3n}\cdot 8={2}^{6}[/latex]
For the following exercises, use logarithms to solve.
63. [latex]{9}^{x-10}=1[/latex]
64. [latex]2{e}^{6x}=13[/latex]
65. [latex]{e}^{r+10}-10=-42[/latex]
66. [latex]2\cdot {10}^{9a}=29[/latex]
67. [latex]-8\cdot {10}^{p+7}-7=-24[/latex]
68. [latex]7{e}^{3n-5}+5=-89[/latex]
69. [latex]{e}^{-3k}+6=44[/latex]
70. [latex]-5{e}^{9x-8}-8=-62[/latex]
71. [latex]-6{e}^{9x+8}+2=-74[/latex]
72. [latex]{2}^{x+1}={5}^{2x-1}[/latex]
73. [latex]{e}^{2x}-{e}^{x}-132=0[/latex]
74. [latex]7{e}^{8x+8}-5=-95[/latex]
75. [latex]10{e}^{8x+3}+2=8[/latex]
76. [latex]4{e}^{3x+3}-7=53[/latex]
77. [latex]8{e}^{-5x-2}-4=-90[/latex]
78. [latex]{3}^{2x+1}={7}^{x-2}[/latex]
79. [latex]{e}^{2x}-{e}^{x}-6=0[/latex]
80. [latex]3{e}^{3-3x}+6=-31[/latex]
For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation
81. [latex]\mathrm{log}\left(\frac{1}{100}\right)=-2[/latex]
82. [latex]{\mathrm{log}}_{324}\left(18\right)=\frac{1}{2}[/latex]
For the following exercises, use the definition of a logarithm to solve the equation.
83. [latex]5{\mathrm{log}}_{7}n=10[/latex]
84. [latex]-8{\mathrm{log}}_{9}x=16[/latex]
85. [latex]4+{\mathrm{log}}_{2}\left(9k\right)=2[/latex]
86. [latex]2\mathrm{log}\left(8n+4\right)+6=10[/latex]
87. [latex]10-4\mathrm{ln}\left(9-8x\right)=6[/latex]
For the following exercises, use the one-to-one property of logarithms to solve.
88. [latex]\mathrm{ln}\left(10-3x\right)=\mathrm{ln}\left(-4x\right)[/latex]
89. [latex]{\mathrm{log}}_{13}\left(5n-2\right)={\mathrm{log}}_{13}\left(8-5n\right)[/latex]
90. [latex]\mathrm{log}\left(x+3\right)-\mathrm{log}\left(x\right)=\mathrm{log}\left(74\right)[/latex]
91. [latex]\mathrm{ln}\left(-3x\right)=\mathrm{ln}\left({x}^{2}-6x\right)[/latex]
92. [latex]{\mathrm{log}}_{4}\left(6-m\right)={\mathrm{log}}_{4}3m[/latex]
93. [latex]\mathrm{ln}\left(x-2\right)-\mathrm{ln}\left(x\right)=\mathrm{ln}\left(54\right)[/latex]
94. [latex]{\mathrm{log}}_{9}\left(2{n}^{2}-14n\right)={\mathrm{log}}_{9}\left(-45+{n}^{2}\right)[/latex]
95. [latex]\mathrm{ln}\left({x}^{2}-10\right)+\mathrm{ln}\left(9\right)=\mathrm{ln}\left(10\right)[/latex]
For the following exercises, solve each equation for[latex]\,x.[/latex]
96. [latex]\mathrm{log}\left(x+12\right)=\mathrm{log}\left(x\right)+\mathrm{log}\left(12\right)[/latex]
97. [latex]\mathrm{ln}\left(x\right)+\mathrm{ln}\left(x-3\right)=\mathrm{ln}\left(7x\right)[/latex]
98. [latex]{\mathrm{log}}_{2}\left(7x+6\right)=3[/latex]
99. [latex]\mathrm{ln}\left(7\right)+\mathrm{ln}\left(2-4{x}^{2}\right)=\mathrm{ln}\left(14\right)[/latex]
100. [latex]{\mathrm{log}}_{8}\left(x+6\right)-{\mathrm{log}}_{8}\left(x\right)={\mathrm{log}}_{8}\left(58\right)[/latex]
101.[latex]\mathrm{ln}\left(3\right)-\mathrm{ln}\left(3-3x\right)=\mathrm{ln}\left(4\right)[/latex]
102. [latex]{\mathrm{log}}_{3}\left(3x\right)-{\mathrm{log}}_{3}\left(6\right)={\mathrm{log}}_{3}\left(77\right)[/latex]
Answers to Section 3.1 Odd Problems
1. [latex]\left(x-3\right)\left(7x+2\right)[/latex]
3. [latex]\left(b+2\right)\left(7b+1\right)[/latex]
5. [latex]\left(a+3\right)\left(5a-2\right)[/latex]
7. [latex]\left(2x-1\right)\left(x-2\right)[/latex]
9. [latex]\left(x+7\right)\left(2x+5\right)[/latex]
11. [latex]\left(2b-3\right)\left(b+1\right)[/latex]
13. [latex]\left(k-4\right)\left(4k-1\right)[/latex]
15. [latex]\left(5n+1\right)\left(n+4\right)[/latex]
17. [latex]\left(3z+1\right)\left(3z+4\right)[/latex]
19. [latex]\left(2k−3\right)\left(2k−5\right)[/latex]
21. [latex]\left(5s−4\right)\left(s−1\right)[/latex]
23. [latex]\left(3y+5\right)\left(2y−3\right)[/latex]
25. [latex]\left(2n+3\right)\left(n−15\right)[/latex]
27. [latex]\left(3x+2\right)\left(x+2\right)[/latex]
29. [latex]10\left(6y−1\right)\left(y+5\right)[/latex]
31. [latex]3z\left(8z+3\right)\left(2z−5\right)[/latex]
33. [latex]8\left(2s+3\right)\left(s+1\right)[/latex]
35. [latex]12\left(4y−3\right)\left(y+1\right)[/latex]
37. [latex]a=\frac{3 \pm \sqrt{3}}{2}[/latex]
39. no real solution
41. [latex]a=\frac{-6 \pm \sqrt{26}}{2}[/latex]
43. [latex]-5, \; -4[/latex]
45. [latex]-\frac{1}{3}[/latex]
47. no solution
49. [latex]2[/latex]
51. no solution
53. Determine first if the equation can be rewritten so that each side uses the same base. If so, the exponents can be set equal to each other. If the equation cannot be rewritten so that each side uses the same base, then apply the logarithm to each side and use properties of logarithms to solve.
55. The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.
57. [latex]x=-\frac{1}{3}[/latex]
59. [latex]n=-1[/latex]
61. [latex]b=\frac{6}{5}[/latex]
63. [latex]x=10[/latex]
65. no solution
67. [latex]p=\mathrm{log}\left(\frac{17}{8}\right)-7[/latex]
69. [latex]k=-\frac{\mathrm{ln}\left(38\right)}{3}[/latex]
71. [latex]x=\frac{\mathrm{ln}\left(\frac{38}{3}\right)-8}{9}[/latex]
73. [latex]x=\mathrm{ln}12\text{ }[/latex]
75. [latex]x=\frac{\mathrm{ln}\left(\frac{3}{5}\right)-3}{8}[/latex]
77. no solution
79. [latex]x=\mathrm{ln}\left(3\right)[/latex]
81. [latex]{10}^{-2}=\frac{1}{100}[/latex]
83. [latex]n=49[/latex]
85. [latex]k=\frac{1}{36}[/latex]
87. [latex]x=\frac{9-e}{8}[/latex]
89. [latex]n=1[/latex]
91. no solution
93. no solution
95. [latex]x=±\frac{10}{3}[/latex]
97. [latex]x=10[/latex]
99. [latex]x=0[/latex]
101. [latex]x=\frac{3}{4}[/latex]