Section 2.2: Simplifying Difference Quotients
This content comes directly from OpenStax’s textbook Algebra and Trigonometry Section 3.3 Rates of Change and Behavior of Graphs.
Learning Objectives
In this section, you will:
- Find the average rate of change of a function.
- Algebraically simplify difference quotients.
Let’s Get Started…
Gasoline costs have experienced some wild fluctuations over the last several decades. Table 1 lists the average cost, in dollars, of a gallon of gasoline for the years 2005–2012. The cost of gasoline can be considered as a function of year.
| [latex]y[/latex] |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
| [latex]C\left(y\right)[/latex] |
2.31 |
2.62 |
2.84 |
3.30 |
2.41 |
2.84 |
3.58 |
3.68 |
Table 1
If we were interested only in how the gasoline prices changed between 2005 and 2012, we could compute that the cost per gallon had increased from $2.31 to $3.68, an increase of $1.37. While this is interesting, it might be more useful to look at how much the price changed per year. In this section, we will investigate changes such as these.
Finding the Average Rate of Change of a Function
The price change per year is a rate of change because it describes how an output quantity changes relative to the change in the input quantity. We can see that the price of gasoline in Table 1 did not change by the same amount each year, so the rate of change was not constant. If we use only the beginning and ending data, we would be finding the average rate of change over the specified period of time. To find the average rate of change, we divide the change in the output value by the change in the input value.
[latex]\begin{array}{ccc}\hfill \text{Average rate of change}& =& \frac{\text{Change in output}}{\text{Change in input}}\hfill \\ & =& \frac{\Delta y}{\Delta x}\hfill \\ & =& \frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =& \frac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}\hfill \end{array}[/latex]
The Greek letter[latex]\text{Δ}\,[/latex](delta) signifies the change in a quantity; we read the ratio as “delta-y over delta-x” or “the change in[latex]\,y\,[/latex]divided by the change in[latex]\,x.[/latex]” Occasionally we write[latex]\,\text{Δ}f\,[/latex]instead of[latex]\,\text{Δ}y,\,[/latex]which still represents the change in the function’s output value resulting from a change to its input value. It does not mean we are changing the function into some other function.
In our example, the gasoline price increased by $1.37 from 2005 to 2012. Over 7 years, the average rate of change was
[latex]\frac{\text{Δ}y}{\text{Δ}x}=\frac{\text{\$}1.37}{\text{7 years}}\approx 0.196\text{ dollars per year}[/latex]
On average, the price of gas increased by about 19.6¢ each year.
Other examples of rates of change include:
- A population of rats increasing by 40 rats per week
- A car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
- A car driving 27 miles per gallon (distance traveled changes by 27 miles for each gallon)
- The current through an electrical circuit increasing by 0.125 amperes for every volt of increased voltage
- The amount of money in a college account decreasing by $4,000 per quarter
Rate of Change
A rate of change describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are “output units per input units.”
The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.
[latex]\frac{\Delta y}{\Delta x}=\frac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}[/latex]
How To
Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values[latex]\,{x}_{1}\,[/latex]and[latex]\,{x}_{2}.[/latex]
- Calculate the difference [latex]{y}_{2}-{y}_{1}=\text{Δ}y.[/latex]
- Calculate the difference [latex]{x}_{2}-{x}_{1}=\text{Δ}x.[/latex]
- Find the ratio[latex]\,\frac{\text{Δ}y}{\text{Δ}x}.[/latex]
EXAMPLE 1
Computing an Average Rate of Change
Using the data in Table 1, find the average rate of change of the price of gasoline between 2007 and 2009.
Show/Hide Solution
 Solution
Solution
In 2007, the price of gasoline was $2.84. In 2009, the cost was $2.41. The average rate of change is
[latex]\begin{array}{ccc}\hfill \frac{\Delta y}{\Delta x}& =& \frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =& \frac{$2.41-$2.84}{2009-2007}\hfill \\ & =& \frac{-$0.43}{2\text{ years}}\hfill \\ & =& -\$0.22\text{ per year}\hfill \end{array}[/latex]
 Try It #1
Try It #1
Using the data in Table 1, find the average rate of change between 2005 and 2010.
EXAMPLE 2
Computing Average Rate of Change from a Graph
Given the function[latex]\,g\left(t\right)\,[/latex]shown in Figure 1, find the average rate of change on the interval[latex]\,\left[-1,2\right].[/latex]
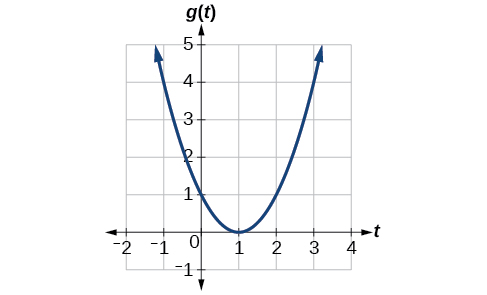
Figure 1
Show/Hide Solution
 Solution
Solution
At [latex]t=-1,[/latex] Figure 2 shows [latex]g\left(-1\right)=4.[/latex] At[latex]\,t=2,[/latex]the graph shows [latex]g\left(2\right)=1.[/latex]
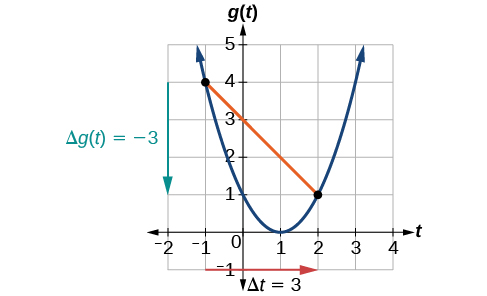
Figure 2
The horizontal change[latex]\,\text{Δ}t=3\,[/latex]is shown by the red arrow, and the vertical change [latex]\text{Δ}g\left(t\right)=-3[/latex] is shown by the turquoise arrow. The average rate of change is shown by the slope of the orange line segment. The output changes by –3 while the input changes by 3, giving an average rate of change of
[latex]\frac{1-4}{2-\left(-1\right)}=\frac{-3}{3}=-1[/latex]
 Analysis
Analysis
Note that the order we choose is very important. If, for example, we use[latex]\,\frac{{y}_{2}-{y}_{1}}{{x}_{1}-{x}_{2}},\,[/latex]we will not get the correct answer. Decide which point will be 1 and which point will be 2, and keep the coordinates fixed as[latex]\,\left({x}_{1},{y}_{1}\right)\,[/latex] and[latex]\,\left({x}_{2},{y}_{2}\right).[/latex]
EXAMPLE 3
Computing Average Rate of Change from a Table
After picking up a friend who lives 10 miles away and leaving on a trip, Anna records her distance from home over time. The values are shown in Table 2. Find her average speed over the first 6 hours.
| [latex]t[/latex](hours) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| [latex]D\left(t\right)[/latex] (miles) |
10 |
55 |
90 |
153 |
214 |
240 |
292 |
300 |
Table 2
Show/Hide Solution
 Solution
Solution
Here, the average speed is the average rate of change. She traveled 282 miles in 6 hours.
[latex]\begin{array}{ccc}\hfill \frac{292-10}{6-0}& =& \frac{282}{6}\hfill \\ & =& 47\hfill \end{array}[/latex]
 Analysis
Analysis
Because the speed is not constant, the average speed depends on the interval chosen. For the interval [2,3], the average speed is 63 miles per hour.
EXAMPLE 4
Computing Average Rate of Change for a Function Expressed as a Formula
Compute the average rate of change of [latex]f\left(x\right)={x}^{2}-\frac{1}{x}[/latex] on the interval [latex]\text{[2,}\,\text{4].}[/latex]
Show/Hide Solution
 Solution
Solution
We can start by computing the function values at each endpoint of the interval.
[latex]\begin{array}{cccccc}\hfill f\left(2\right)& =& {2}^{2}-\frac{1}{2}\hfill & \hfill \phantom{\rule{2em}{0ex}}f\left(4\right)& =& {4}^{2}-\frac{1}{4}\hfill \\ & =& 4-\frac{1}{2}\hfill & & =& 16-\frac{1}{4}\hfill \\ & =& \frac{7}{2}\hfill & & =& \frac{63}{4}\hfill \end{array}[/latex]
Now we compute the average rate of change.
[latex]\begin{array}{ccc}\hfill \text{Average rate of change}& =& \frac{f\left(4\right)-f\left(2\right)}{4-2}\hfill \\ & =& \frac{\frac{63}{4}-\frac{7}{2}}{4-2}\hfill \\ & =& \frac{\frac{49}{4}}{2}\hfill \\ & =& \frac{49}{8}\hfill \end{array}[/latex]
 Try It #2
Try It #2
Find the average rate of change of [latex]f\left(x\right)=x-2\sqrt{x}[/latex] on the interval [latex]\left[1,\,9\right].[/latex]
EXAMPLE 5
Finding the Average Rate of Change of a Force
The electrostatic force[latex]\,F,[/latex]measured in newtons, between two charged particles can be related to the distance between the particles[latex]\,d,[/latex]in centimeters, by the formula[latex]\,F\left(d\right)=\frac{2}{{d}^{2}}.[/latex]Find the average rate of change of force if the distance between the particles is increased from 2 cm to 6 cm.
Show/Hide Solution
 Solution
Solution
We are computing the average rate of change of[latex]\,F\left(d\right)=\frac{2}{{d}^{2}}\,[/latex]on the interval[latex]\,\left[2,6\right].[/latex]
[latex]\begin{array}{cccc}\hfill \text{Average rate of change}& =& \text{ }\frac{F\left(6\right)-F\left(2\right)}{6-2}\hfill & \\ & =& \frac{\frac{2}{{6}^{2}}-\frac{2}{{2}^{2}}}{6-2}\hfill & \text{Simplify}.\hfill \\ & =\hfill & \frac{\frac{2}{36}-\frac{2}{4}}{4}\hfill & \\ & =& \frac{-\frac{16}{36}}{4}\hfill & \text{Combine numerator terms}.\hfill \\ & =& -\frac{1}{9}\hfill & \text{Simplify}\hfill \end{array}[/latex]
The average rate of change is [latex]-\frac{1}{9}[/latex] newton per centimeter.
EXAMPLE 6
Finding the Average Rate of Change of a Force
Find the average rate of change of [latex]g\left(t\right)={t}^{2}+3t+1[/latex] on the interval [latex]\left[0,\,a\right].[/latex] The answer will be an expression involving [latex]a[/latex] in simplest form.
Show/Hide Solution
 Solution
Solution
We use the average rate of change formula.
[latex]\begin{array}{cccc}\hfill \text{Average rate of change}& =& \frac{g\left(a\right)-g\left(0\right)}{a-0}\hfill & \text{Evaluate}.\hfill \\ & =& \frac{\left({a}^{2}+3a+1\right)-\left({0}^{2}+3\left(0\right)+1\right)}{a-0}\hfill & \text{Simplify}.\hfill \\ & =& \frac{{a}^{2}+3a+1-1}{a}\hfill & \text{Simplify and factor}.\hfill \\ & =& \frac{a\left(a+3\right)}{a}\hfill & \text{Divide by the common factor }a.\hfill \\ & =& a+3\hfill & \end{array}[/latex]
This result tells us the average rate of change in terms of[latex]\,a\,[/latex]between[latex]\,t=0\,[/latex]and any other point[latex]\,t=a.\,[/latex]
For example, on the interval[latex]\,\left[0,5\right],\,[/latex]the average rate of change would be[latex]\,5+3=8.[/latex]
 Try It #3
Try It #3
Find the average rate of change of[latex]\,f\left(x\right)={x}^{2}+2x-8\,[/latex] on the interval[latex]\,\left[5,a\right]\,[/latex]in simplest forms in terms of [latex]a[/latex].
Section 2.2 Exercises
[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]
Verbal
1. Can the average rate of change of a function be constant?
2. Can the average rate of change of a function be a function?
Algebraic
For the following exercises, find the average rate of change of each function on the interval specified for real numbers [latex]\,b\,[/latex]or[latex]\,h[/latex] in simplest form.
3. [latex]f\left(x\right)=4{x}^{2}-7\,[/latex]on[latex]\,\left[1,\text{ }b\right][/latex]
4. [latex]g\left(x\right)=2{x}^{2}-9\,[/latex]on[latex]\,\left[4,\text{ }b\right][/latex]
5. [latex]p\left(x\right)=3x+4\,[/latex]on[latex]\,\left[2,\text{ }2+h\right][/latex]
6. [latex]k\left(x\right)=4x-2\,[/latex]on[latex]\,\left[3,\text{ }3+h\right][/latex]
7. [latex]f\left(x\right)=2{x}^{2}+1\,[/latex]on[latex]\,\left[x,x+h\right][/latex]
8. [latex]g\left(x\right)=3{x}^{2}-2\,[/latex]on[latex]\,\left[x,x+h\right][/latex]
9. [latex]a\left(t\right)=\frac{1}{t+4}\,[/latex]on[latex]\,\left[9,9+h\right][/latex]
10. [latex]b\left(x\right)=\frac{1}{x+3}\,[/latex]on[latex]\,\left[1,1+h\right][/latex]
11. [latex]j\left(x\right)=3{x}^{3}\,[/latex]on[latex]\,\left[1,1+h\right][/latex]
12. [latex]r\left(t\right)=4{t}^{3}\,[/latex]on[latex]\,\left[2,2+h\right][/latex]
13. [latex]\frac{f\left(x+h\right)-f\left(x\right)}{h}\,[/latex]given[latex]\,f\left(x\right)=2{x}^{2}-3x\,[/latex]on[latex]\,\left[x,x+h\right][/latex]
Numeric
14. Table 3 gives the annual sales (in millions of dollars) of a product from 1998 to 2006. What was the average rate of change of annual sales (a) between 2001 and 2002, and (b) between 2001 and 2004?
| Year |
Sales
(millions of dollars) |
| 1998 |
201 |
| 1999 |
219 |
| 2000 |
233 |
| 2001 |
243 |
| 2002 |
249 |
| 2003 |
251 |
| 2004 |
249 |
| 2005 |
243 |
| 2006 |
233 |
Table 3
15. Table 4 gives the population of a town (in thousands) from 2000 to 2008. What was the average rate of change of population (a) between 2002 and 2004, and (b) between 2002 and 2006?
| Year |
Population
(thousands) |
| 2000 |
87 |
| 2001 |
84 |
| 2002 |
83 |
| 2003 |
80 |
| 2004 |
77 |
| 2005 |
76 |
| 2006 |
78 |
| 2007 |
81 |
| 2008 |
85 |
Table 4
For the following exercises, find the average rate of change of each function on the interval specified.
16. [latex]f\left(x\right)={x}^{2}\,[/latex]on[latex]\,\left[1,\text{ }5\right][/latex]
17. [latex]h\left(x\right)=5-2{x}^{2}\,[/latex]on[latex]\,\left[-2,\text{4}\right][/latex]
18. [latex]q\left(x\right)={x}^{3}\,[/latex]on[latex]\,\left[-4,\text{2}\right][/latex]
19. [latex]g\left(x\right)=3{x}^{3}-1\,[/latex]on[latex]\,\left[-3,\text{3}\right][/latex]
20. [latex]y=\frac{1}{x}\,[/latex]on[latex]\,\left[1,\text{ 3}\right][/latex]
21. [latex]p\left(t\right)=\frac{\left({t}^{2}-4\right)\left(t+1\right)}{{t}^{2}+3}\,[/latex]on[latex]\,\left[-3,\text{1}\right][/latex]
22. [latex]k\left(t\right)=6{t}^{2}+\frac{4}{{t}^{3}}\,[/latex]on[latex]\,\left[-1,3\right][/latex]
Real-World Applications
23. A driver of a car stopped at a gas station to fill up his gas tank. He looked at his watch, and the time read exactly 3:40 p.m. At this time, he started pumping gas into the tank. At exactly 3:44, the tank was full and he noticed that he had pumped 10.7 gallons. What is the average rate of flow of the gasoline into the gas tank?
24. Near the surface of the moon, the distance that an object falls is a function of time. It is given by[latex]\,d\left(t\right)=2.6667{t}^{2},\,[/latex]where[latex]\,t\,[/latex]is in seconds and[latex]\,d\left(t\right)\,[/latex]is in feet. If an object is dropped from a certain height, find the average velocity of the object from[latex]\,t=1\,[/latex]to[latex]\,t=2.[/latex]
25. The graph in Figure 3 illustrates the decay of a radioactive substance over[latex]\,t\,[/latex]days.
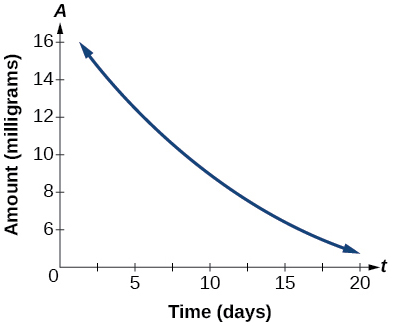
Figure 3
Use the graph to estimate the average decay rate from[latex]\,t=5\,[/latex]to[latex]\,t=15.[/latex]
Answers to Section 2.2 Odd Problems
1. Yes, the average rate of change of all linear functions is constant.
3. 4(b+1)
5. 3
7. 4x+2h
9. −113(13+h)
11. 3h2+9h+9
13. 4x+2h−3
15.
ⓐ –3000
ⓑ –1250
17. -4
19. 27
21. –0.167
23. 2.7 gallons per minute
25. approximately –0.6 milligrams per day






