Learning Objectives
In this section, you will:
- Use the exponent and [latex]e[/latex] keys on your calculator.
- Know the definition of an exponential function.
- Evaluate an exponential function.
- Graph exponential functions.
In this section, you will:
The function[latex]f[/latex] defined by
[latex]f\left(x\right)={b}^{x}[/latex]
where [latex]b[/latex] > [latex]0[/latex], [latex]b\ne1[/latex], and the exponent [latex]x[/latex] is any real number, is called an exponential function.
Also, note that in this definition, the base [latex]b[/latex] is restricted to being a positive number other than 1.
Use the caret top key to calculate 15 raised to the 5th power.
Use [latex]{x}^{y}[/latex] or [latex]{y}^{x}[/latex] to calculate 15 raised to the 5th power.
The exponential function[latex]f[/latex] with base [latex]e[/latex],
[latex]f\left(x\right)={e}^{x}[/latex],
is called the natural exponential function. [latex]e[/latex] is a special number with a value of approximately 2.718281828…
Use [latex]e[/latex] key with the caret top key to calculate [latex]e[/latex] raised to the 5th power.
The key that looks like [latex]{e}^{x}[/latex] is most common in business and scientific calculators, but can be found on other types of calculators. Note that the difference between this key and the [latex]e[/latex] key above is that [latex]{e}^{x}[/latex] has a variable exponent showing on the key. The [latex]e[/latex] key above only has an [latex]e[/latex] with no exponent.
Use the [latex]{e}^{x}[/latex] key to calculate [latex]e[/latex] raised to the 5th power.
As mentioned above, there are a lot of different types of calculators out there. I want to mention a few things about putting in formulas.
Most graphing calculators allow you to put in the whole formula before you press enter. In fact, you are able to see it all. If you are going to plug in the whole formula at one time, just make sure you are careful. Pay special attention to putting in the parenthesis in the right place.
On most business and scientific calculators, you will have to put the formula in part by part. Work your way inside out of the parenthesis. DO NOT round until you are at the end. As you go step by step, don’t erase what you have on your calculator screen. Use it in the next step so you will have the full decimal number.
DO NOT round until you get to the final answer. You will note on a lot of the examples that I put dots after my numbers that would keep going on an on if I had more space on my calculator. Keep in mind that your calculator may have fewer or more spaces than my calculator does – so your calculator may have a slightly different answer than mine, due to rounding. It should be very close though.
Approximate the number [latex]{e}^{7.25}[/latex] using a calculator. Round to four decimal places.
 Solution
Solution[latex]{e}^{7.25}\approx1408.1048[/latex]
Approximate the number [latex]{e}^{-0.12}[/latex] using a calculator. Round to four decimal places.
 Solution
Solution[latex]{e}^{-0.12}\approx0.8869[/latex]
The process of graphing any exponential function follows the same 3 basic steps.
I have found that the best way to do this is to do it the same each time. In other words, put in the same values for [latex]x[/latex] each time and then find the corresponding [latex]y-[/latex]value for the given function.
 OR
OR
Graph the function [latex]f\left(x\right)={4}^{x}[/latex].
 Solution
SolutionNote that the base = 4 and the exponent is our variable [latex]x[/latex]. Also note, that it is in the basic form given by the definition above. In other words, there are no other factors effecting this function.
| [latex]x[/latex] | [latex]f\left(x\right)={4}^{x}[/latex] |
| [latex]-2[/latex] | [latex]f\left(-2\right)={4}^{-2}=\frac{1}{{4}^{2}}=\frac{1}{16}=0.0625[/latex] |
| [latex]-1[/latex] | [latex]f\left(-1\right)={4}^{-1}=\frac{1}{{4}^{1}}=\frac{1}{4}=0.25[/latex] |
| [latex]0[/latex] | [latex]f\left(0\right)={4}^{0}=1[/latex] |
| [latex]1[/latex] | [latex]f\left(1\right)={4}^{1}=4[/latex] |
| [latex]2[/latex] | [latex]f\left(2\right)={4}^{2}=16[/latex] |
This gives the ordered pairs: [latex]\left(-2,0.0625\right), \left(-1,0.25\right), \left(0,1\right), \left(1,4\right), \text{and} \left(2,16\right).[/latex]
First, plot the 5 points above on a set of [latex]x-y[/latex] axes. Then, connect the points with a smooth, exponential curve.
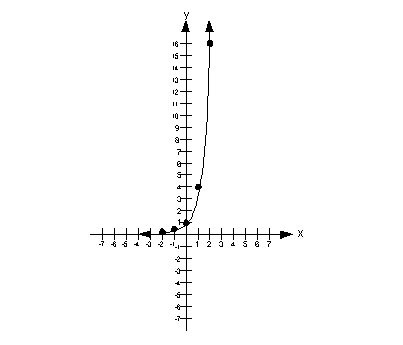
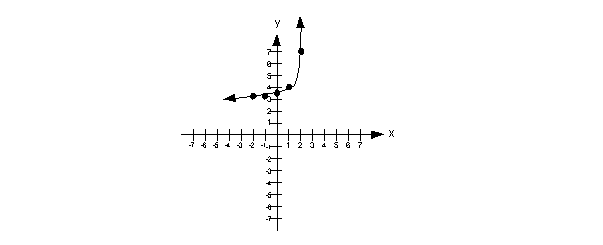
Graph the function [latex]f\left(x\right)={4}^{x-1}+3[/latex].
 Solution
SolutionNote that the base = 4, and the exponent is [latex]x - 1.[/latex] There are two outside factors: we are subtracting 1 from our variable [latex]x[/latex] in the exponent, AND we are adding 3 to our base after we raise it to the exponent [latex]x - 1.[/latex]
| [latex]x[/latex] | [latex]f\left(x\right)={4}^{x-1}+3[/latex] |
| [latex]-2[/latex] | [latex]f\left(-2\right)={4}^{-2-1}+3=\frac{1}{{4}^{3}}+3=\frac{1}{64}+3=3.015625[/latex] |
| [latex]-1[/latex] | [latex]f\left(-1\right)={4}^{-1-1}+3=\frac{1}{{4}^{2}}+3=\frac{1}{16}+3=3.0625[/latex] |
| [latex]0[/latex] | [latex]f\left(0\right)={4}^{0-1}+3=\frac{1}{{4}^{1}}+3=\frac{1}{4}+3=3.25[/latex] |
| [latex]1[/latex] | [latex]f\left(1\right)={4}^{1-1}+3={4}^{0}+3=1+3=4[/latex] |
| [latex]2[/latex] | [latex]f\left(2\right)={4}^{2-1}+3={4}^{1}+3=4+3=7[/latex] |
This gives the ordered pairs: [latex]\left(-2,3.015625\right), \left(-1,3.0625\right), \left(0,3.25\right), \left(1,4\right), \text{and} \left(2,7\right).[/latex]
First, plot the 5 points above on a set of [latex]x-y[/latex] axes. Then, connect the points with a smooth, exponential curve.
Graph the function [latex]f\left(x\right)=4\left(\frac{1}{4}\right)^{x}-3[/latex].
 Solution
SolutionBe careful that you use the order of operations when working a problem like this. We need to deal with the exponent first BEFORE we multiply by 4. It is really tempting to cross out the 4 on the outside with the 4 in the denominator of our base. But the 4 in the denominator is enclosed by ( ), with an exponent attached to it. So, we have to deal with that first before getting the 4 on the outside involved.
| [latex]x[/latex] | [latex]f\left(x\right)=4\left(\frac{1}{4}\right)^{x}-3[/latex] |
| [latex]-2[/latex] | [latex]f\left(-2\right)=4\left(\frac{1}{4}\right)^{-2}-3=4\left({4}\right)^{2}-3=4\left(16\right)-3=64-3=61[/latex] |
| [latex]-1[/latex] | [latex]f\left(-1\right)=4\left(\frac{1}{4}\right)^{-1}-3=4\left({4}\right)^{1}-3=4\left(4\right)-3=16-3=13[/latex] |
| [latex]0[/latex] | [latex]f\left(0\right)=4\left(\frac{1}{4}\right)^{0}-3=4\left(1\right)-3=4-3=1[/latex] |
| [latex]1[/latex] | [latex]f\left(1\right)=4\left(\frac{1}{4}\right)^{1}-3=4\left(\frac{1}{4}\right)-3=1-3=-2[/latex] |
| [latex]2[/latex] | [latex]f\left(2\right)=4\left(\frac{1}{4}\right)^{2}-3=4\left(\frac{1}{16}\right)-3=\frac{4}{16}-3=-2.75[/latex] |
This gives the ordered pairs: [latex]\left(-2,61\right), \left(-1,13\right), \left(0,1\right), \left(1,-2\right), \text{and} \left(2,-2.75\right).[/latex]
First, plot the 5 points above on a set of [latex]x-y[/latex] axes. Then, connect the points with a smooth, exponential curve.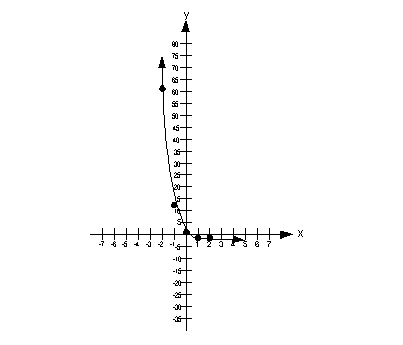
In this section, you will:
The logarithmic function with base [latex]b[/latex], where [latex]b\,[/latex]>[latex]\,0[/latex] and [latex]b\ne1[/latex], is defined by
[latex]y=\log_{b}\left(x\right)[/latex]
if and only if
[latex]{b}^{y}=x.[/latex]
This definition can work in both directions. In some cases you will have an equation written in log form and need to convert it to exponential form and vice versa.
So, when you are converting from log form to exponential form, [latex]b[/latex] is your base, [latex]y[/latex] IS YOUR EXPONENT, and [latex]x[/latex] is what your exponential expression is set equal to.
Note that your domain is all positive real numbers and range is all real numbers.
Express the logarithmic equation [latex]3=\log_{5}\left(125\right)[/latex] exponentially.
 Solution
SolutionFirst, let’s figure out what the base needs to be. What do you think? It looks like the [latex]b[/latex] in the definition correlates with 5 in our problem – so our base is going to be 5.
Next, let’s figure out the exponent. This is very key. Again, remember that logs are another way to write exponents. This means the log is set equal to the exponent. So, in this problem, that means that the exponent has to be 3.
That leaves 125 to be what the exponential expression is set equal to.
Putting all of this into the log definition we get:
[latex]3=\log_{5}\left(125\right)\,\,\Rightarrow\,\,{5}^{3}=125.[/latex]
Express the logarithmic equation [latex]\log_{7}\left(49\right)=y[/latex] exponentially.
 Solution
SolutionFirst, let’s figure out what the base needs to be. What do you think? It looks like the [latex]b[/latex] in the definition correlates with 7 in our problem – so our base is going to be 7.
Next, let’s figure out the exponent. This is very key. Again, remember that logs are another way to write exponents. This means the log is set equal to the exponent. So, in this problem, that means that the exponent has to be [latex]y[/latex].
That leaves 49 to be what the exponential expression is set equal to.
Putting all of this into the log definition we get:
[latex]\log_{7}\left(49\right)=y\,\,\Rightarrow\,\,{7}^{y}=49.[/latex]
Express the exponential equation [latex]{6}^{-2}=\frac{1}{36}[/latex] in logarithmic form.
 Solution
SolutionFirst, let’s figure out what the base needs to be. What do you think? It looks like the [latex]b[/latex] in the definition correlates with 6 in our problem – so our base is going to be 6.
Next, let’s figure out the exponent. In this direction it is easy to note what the exponent is because we are more used to it written in this form. However, when we write it in the log form, we have to be careful to place it correctly. Looks like the exponent is -2, don’t you agree?
The value that the exponential expression is set equal to is what goes inside the log function. In this problem that is [latex]\frac{1}{36}[/latex].
Let’s see what we get when we put this in log form:
[latex]{6}^{-2}=\frac{1}{36}\,\,\Rightarrow\,\,-2=\log_{6}\left(\frac{1}{36}\right).[/latex]
Express the exponential equation [latex]\sqrt{81}=x[/latex] in logarithmic form.
 Solution
SolutionRewriting the original problem using exponents, we get:
[latex]\sqrt{81}={81}^{\frac{1}{2}}.[/latex]
Now, let’s figure out what the base needs to be. What do you think? It looks like the [latex]b[/latex] in the definition correlates with 81 in our problem – so our base is going to be 81.
Next, let’s figure out the exponent. In this direction it is easy to note what the exponent is because we are more used to it written in this form. However, when we write it in the log form, we have to be careful to place it correctly. Looks like the exponent is [latex]\frac{1}{2},[/latex] don’t you agree?
The value that the exponential expression is set equal to is what goes inside the log function. In this problem that is [latex]x[/latex].
Let’s see what we get when we put this in log form:
[latex]\sqrt{81}\,\,\Rightarrow\,\,{81}^{\frac{1}{2}}=x\,\,\Rightarrow\,\,\frac{1}{2}=\log_{81}\left(x\right).[/latex]
The process of evaluating logs follows the same 3 basic steps.
Evaluate a logarithm.
Evaluate the expression [latex]\log_{6}\left(64\right)[/latex] without using a calculator.
 Solution
Solution[latex]\log_{4}\left(64\right)=x[/latex]
[latex]{4}^{x}=64[/latex]
Since 3 is the exponent of [latex]4[/latex] we need to get 64, we know that:
[latex]x=3.[/latex]
EXAMPLE 6
Evaluate the expression [latex]\log_{9}\left(1\right)[/latex] without using a calculator.
 Solution
Solution[latex]\log_{9}\left(1\right)=x[/latex]
[latex]{9}^{x}=1[/latex]
Since 0 is the exponent of [latex]9[/latex] we need to get 1, we know that:
[latex]x=0.[/latex]
EXAMPLE 7
Evaluate the expression [latex]\log_{7}\left(7\right)[/latex] without using a calculator.
 Solution
Solution[latex]\log_{7}\left(7\right)=x[/latex]
[latex]{7}^{x}=7[/latex]
Since 1 is the exponent of [latex]7[/latex] we need to get 7, we know that:
[latex]x=1.[/latex]
EXAMPLE 8
Evaluate the expression [latex]\log_{5}\left(\sqrt{5}\right)[/latex] without using a calculator.
 Solution
Solution[latex]\log_{5}\left(\sqrt{5}\right)=x[/latex]
[latex]{5}^{x}=\sqrt{5}[/latex]
Since [latex]\frac{1}{2}[/latex] is the exponent of [latex]5[/latex] we need to get [latex]\sqrt{5}[/latex], we know that:
[latex]x=\frac{1}{2}.[/latex]
The process of graphing any logarithmic function follows the same 4 basic steps.
You have to be careful that you note that the [latex]log[/latex] key on your calculator is only for base 10 and your [latex]ln[/latex] key is only for base [latex]e.[/latex] So if you have any other base, you would not be able to use your calculator. But, if you write a logarithm in exponential form, you can enter in any base in your calculator – that is why we do step 1.
Note that this is what we call an inverse function of the exponential function. They are inverses because the [latex]x-[/latex] and [latex]y-[/latex]values are switched. In the exponential functions, the [latex]x-[/latex]value was the exponent, but in the log functions, the [latex]y-[/latex]value is the exponent. The [latex]y-[/latex]value is what the exponential function is set equal to, but in the log functions it ends up being set equal to [latex]x.[/latex] So that is why in step 2, we will be plugging in for [latex]y[/latex] instead of [latex]x[/latex].
 OR
OR
Graph the function [latex]y=f\left(x\right)=\log_{3}\left(x\right).[/latex]
 Solution
SolutionLooks like the base is 3, the exponent is [latex]y[/latex], and the exponential form will be set = to [latex]x[/latex]:
[latex]{3}^{y}=x[/latex]
| [latex]{3}^{y}=x[/latex] | [latex]y[/latex] |
| [latex]{3}^{-2}=\frac{1}{{3}^{2}}=\frac{1}{9}[/latex] | [latex]-2[/latex] |
| [latex]{3}^{-1}=\frac{1}{{3}^{1}}=\frac{1}{3}[/latex] | [latex]-1[/latex] |
| [latex]{3}^{0}=1[/latex] | [latex]0[/latex] |
| [latex]{3}^{1}=3[/latex] | [latex]1[/latex] |
| [latex]{3}^{2}=9[/latex] | [latex]2[/latex] |
This gives the ordered pairs: [latex]\left(\frac{1}{9},-2\right), \left(\frac{1}{3},-1\right), \left(1,0\right), \left(3,1\right), \text{and} \left(9,2\right).[/latex]
First, plot the 5 points above on a set of [latex]x-y[/latex] axes. Then, connect the points with a smooth, exponential curve.
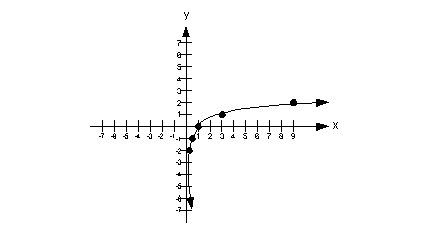
Graph the function [latex]y=f\left(x\right)=\log_{3}\left(x+1\right).[/latex]
 Solution
SolutionLooks like the base is 3, the exponent is [latex]y[/latex], and the exponential form will be set = to [latex]x+1[/latex]:
[latex]{3}^{y}=x+1[/latex]
or
[latex]{3}^{y}-1=x[/latex]
| [latex]{3}^{y}-1=x[/latex] | [latex]y[/latex] |
| [latex]{3}^{-2}-1=\frac{1}{{3}^{2}}-1=\frac{1}{9}-1=-\frac{8}{9}[/latex] | [latex]-2[/latex] |
| [latex]{3}^{-1}-1=\frac{1}{{3}^{1}}-1=\frac{1}{3}-1=-\frac{2}{3}[/latex] | [latex]-1[/latex] |
| [latex]{3}^{0}-1=1-1=0[/latex] | [latex]0[/latex] |
| [latex]{3}^{1}-1=3-1=2[/latex] | [latex]1[/latex] |
| [latex]{3}^{2}-1=9-1=8[/latex] | [latex]2[/latex] |
This gives the ordered pairs: [latex]\left(-\frac{8}{9},-2\right), \left(-\frac{2}{3},-1\right), \left(0,0\right), \left(2,1\right), \text{and} \left(8,2\right).[/latex]
First, plot the 5 points above on a set of [latex]x-y[/latex] axes. Then, connect the points with a smooth, exponential curve.
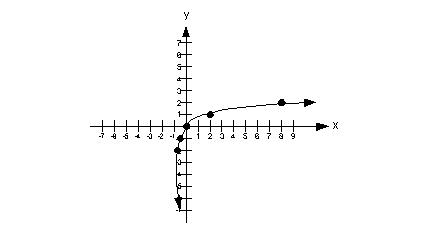
Graph the function [latex]y=f\left(x\right)=-\log_{3}\left(x\right).[/latex]
 Solution
SolutionFirst, let’s rewrite the function to make the side of the equation with the log positive:
[latex]y=-\log_{3}\left(x\right)\,\,\Rightarrow\,\,-y=\log_{3}\left(x\right).[/latex]
Now, it looks like the base is 3, the exponent is [latex]-y[/latex], and the exponential form will be set = to [latex]x[/latex]:
[latex]{3}^{-y}=x[/latex]
| [latex]{3}^{-y}=x[/latex] | [latex]y[/latex] |
| [latex]{3}^{-\left(-2\right)}={3}^{2}=9[/latex] | [latex]-2[/latex] |
| [latex]{3}^{-\left(-1\right)}={3}^{1}=3[/latex] | [latex]-1[/latex] |
| [latex]{3}^{-0}={3}^{0}=1[/latex] | [latex]0[/latex] |
| [latex]{3}^{-1}=\frac{1}{{3}^{1}}=\frac{1}{3}[/latex] | [latex]1[/latex] |
| [latex]{3}^{-2}=\frac{1}{{3}^{2}}=\frac{1}{9}[/latex] | [latex]2[/latex] |
This gives the ordered pairs: [latex]\left(9,-2\right), \left(3,-1\right), \left(1,0\right), \left(\frac{1}{3},1\right), \text{and} \left(\frac{1}{9},2\right).[/latex]
First, plot the 5 points above on a set of [latex]x-y[/latex] axes. Then, connect the points with a smooth, exponential curve.
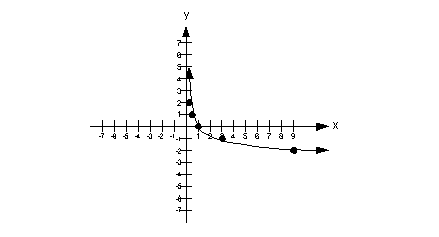
Find the domain of the logarithmic function [latex]f\left(x\right)=\log_{2}\left(5-x\right).[/latex]
 Solution
Solution
That means that if we put in any value of [latex]x[/latex] that is less than 5, we will end up with a positive value inside our log.
Find the domain of the logarithmic function [latex]f\left(x\right)=\log_{2}{\left(2+x\right)}^{2}.[/latex]
 Solution
Solution
That means that, as long as we don’t plug in -2 for [latex]x[/latex], we will end up with a positive value inside our log.
There are 2 inverse properties of logs that can be powerful simplifying tools.
[latex]\log_{b}\left({b}^{r}\right)=r[/latex]
where[latex]\,b\,[/latex] > [latex]0[/latex] and[latex]\,b\ne1.[/latex]
Boy, the definition of logs sure does come in handy to explain these properties. Applying that definition you would have [latex]b[/latex] raised to the [latex]r[/latex] power, which equals [latex]b[/latex] raised to the [latex]r[/latex] power.
Here is a quick illustration of how this property works:
[latex]\log_{5}\left({5}^{\frac{1}{2}}\right)=?[/latex]
[latex]\log_{5}\left({5}^{\frac{1}{2}}\right)=\frac{1}{2}.[/latex]
[latex]{b}^{\log_{b}\left(m\right)}=m[/latex]
where[latex]\,b\,[/latex] > [latex]0[/latex] and[latex]\,b\ne1.[/latex]
This one is a little bit more involved and weird looking huh? Going back to our favorite saying – a log is another way to write exponents – what we have here is the log is the exponent we need to raise [latex]b[/latex] to get [latex]m[/latex]. Well, if we turn around and raise our first base [latex]b[/latex] to that exponent, it stands to reason that we would get [latex]b[/latex].
Here is a quick illustration of how this property works:
[latex]{2}^{\log_{2}\left(3\right)}=?[/latex]
[latex]{2}^{\log_{2}\left(3\right)}=3.[/latex]
There are 2 bases that are the most frequently used for logarithms.
[latex]\log\left(x\right)\,\,\Rightarrow\,\,\log_{10}\left(x\right)[/latex]
When using common log (base 10), use the form [latex]\log\left(x\right)[/latex] to write it.
[latex]\ln\left(x\right)\,\,\Rightarrow\,\,\log_{e}\left(x\right)[/latex]
When using the natural log (base [latex]e[/latex]), use the form [latex]\ln\left(x\right)[/latex] to write it.
EXAMPLE 14
Evaluate [latex]\log\left(0.001\right)[/latex] without using a calculator.
 Solution
Solution
[latex]\log\left(0.001\right)\,\,\Rightarrow\,\,\log\left({10}^{-3}\right)[/latex]
[latex]\log\left({10}^{-3}\right)=?[/latex]
[latex]\log\left({10}^{-3}\right)=-3[/latex]
Evaluate [latex]{e}^{\ln\left(50\right)}[/latex] without using a calculator.
 Solution
Solution
Evaluate [latex]{10}^{\log\left({5x}^{2}\right)}[/latex] without using a calculator.
 Solution
Solution
EXAMPLE 17
Evaluate [latex]\ln\left(\frac{1}{{e}^{x}}\right)[/latex] without using a calculator.
 Solution
Solution
[latex]\ln\left(\frac{1}{{e}^{x}}\right)\,\,\Rightarrow\,\,\ln\left({e}^{-x}\right)[/latex]
[latex]\ln\left({e}^{-x}\right)=?[/latex]
[latex]\ln\left({e}^{-x}\right)=-x[/latex]