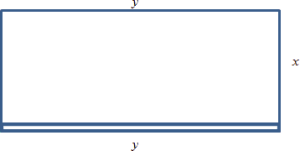Section 3.5:  Decoding Word Problems Involving Optimization

Amy Graham Goodman

Section 3.5: Decoding Word Problems Involving Optimization

This content comes directly from Larry Musolino open textbook Techniques of Calculus 1 Section 4.5 Optimization Applications.

Access this resource for free at https://psu.pb.unizin.org/math110/chapter/4-5-optimization-applications/

Learning Objectives

In this section, you will:

Draw a picture of the scenario a word problem describes.
Define all the variables mentioned in a word problem.
Analyze word problems for “buzz” words and translate them into mathematical notation.
Define the objective function described in a word problem.
Define constraint functions and use them to make the objective function of one variable.

Let’s Get Started Talking About Applied Optimization

We have used derivatives to help find the maximums and minimums of some functions given by equations, but it is very unlikely that someone will simply hand you a function and ask you to find its extreme values. More typically, someone will describe a problem and ask your help in maximizing or minimizing something: What is the largest volume package which the post office will take?; What is the quickest way to get from here to there?; or What is the least expensive way to accomplish some task? In this section, we’ll discuss how to find these extreme values using calculus.

In business applications, we are often interested to maximize revenue, or maximize profit and minimize costs. For example, we can determine the derivative of the profit function and use this analysis to determine conditions to maximize profit levels for a business.

Max/Min Applications

The manager of a garden store wants to build a 600 square foot rectangular enclosure on the store’s parking lot in order to display some equipment. Three sides of the enclosure will be built of redwood fencing, at a cost of $7 per running foot. The fourth side will be built of cement blocks, at a cost of $14 per running foot. Find the dimensions of the least costly such enclosure.

The process of finding maxima or minima is called optimization. The function we’re optimizing is called the objective function (or objective equation). The objective function can be recognized by its proximity to est words (greatest, least, highest, farthest, most, …). Look at the garden store example; the cost function is the objective function.

In many cases, there are two (or more) variables in the problem. In the garden store example again, the length and width of the enclosure are both unknown. If there is an equation that relates the variables we can solve for one of them in terms of the others, and write the objective function as a function of just one variable. Equations that relate the variables in this way are called constraint equations. The constraint equations are always equations, so they will have equals signs. For the garden store, the fixed area relates the length and width of the enclosure. This will give us our constraint equation.

How To

Decode Max-Min Story Problems

Translate the English statement of the problem line by line into a picture (if that applies) and into math. This is often the hardest step!
Identify the objective function. Look for “buzz” words indicating a largest or smallest value.
1. If you seem to have two or more variables, find the constraint equation. Think about the English meaning of the word constraint, and remember that the constraint equation will have an equals sign.
2. Solve the constraint equation for one variable and substitute into the objective function. Now you have an equation of one variable.
Use calculus to find the optimum values. (Take derivative, find critical points, test. Don’t forget to check the endpoints!)
Look back at the question to make sure you answered what was asked. Translate your number answer back into English.

EXAMPLE 1

Decoding Max-Min Story Problems

The manager of a garden store wants to build a 600 square foot rectangular enclosure on the store’s parking lot in order to display some equipment. Three sides of the enclosure will be built of redwood fencing, at a cost of $7 per running foot. The fourth side will be built of cement blocks, at a cost of $14 per running foot. Find the dimensions of the least costly such enclosure.

Show/Hide Solution

Solution

Step 1. Translate line by line into a picture, as in Figure 1, and math.

A rectangle is shown. The top edge is labeled as y. The bottom edge is labeled as y. The right side edge is labeled as x.

Figure 1

Let’s use the variable names from our picture to translate the words from the problem into equations. So, [latex]x[/latex] and [latex]y[/latex] will be the dimensions of the enclosure, with [latex]y[/latex] being the length of the side made of blocks. Then: [latex]\text{Area} = A = xy = 600.[/latex]

[latex]2x + y[/latex] costs $7 per foot, [latex]y[/latex] costs $14 per foot, so

[latex]\text{Cost} = C = 7(2x + y) + 14y = 14x + 21y.[/latex]

Step 2. Identify the objective function.

The “buzz” word in this problem that helps us identify the objective function is “least.” The problem asked for the “least costly enclosure.” That means, we want to find [latex]x[/latex] and [latex]y[/latex] so that [latex]C[/latex] is minimized. A minimum is something we know we can use calculus to find in Step 3. So,

[latex]\begin{array}{cc}\hfill C = 7(2x + y) + 14y = 14x + 21y \hfill & \hfill \text{is our objective function.} \hfill \end{array}[/latex]

As it stands, though, this objective function has two variables. So, we need to use the constraint equation. The constraint equation is the fixed area [latex]A = xy = 600[/latex]. Solve [latex]A[/latex] for [latex]x[/latex] to get [latex]x=\frac{600}{y}[/latex], and then substitute into [latex]C[/latex] to get an objective function of one variable.

[latex]\begin{array}{llll}C \hfill &= & 14\left(\frac{600}{y}\right)+21y \hfill & \\ C\hfill & = & \frac{8400}{y}+21y \hfill & \text{is our objective function of one variable.} \hfill \end{array}[/latex]

Step 3. Use calculus to find the optimum values.

Now that we have a function of just one variable, we can find the minimum using calculus.

[latex]C'=-\frac{8400}{y^2}+21[/latex]

[latex]C'[/latex] is undefined for [latex]y = 0[/latex], and [latex]C' = 0[/latex] when [latex]y = 20[/latex] or [latex]y = -20[/latex].

Of these three critical numbers, only [latex]y = 20[/latex] makes sense (is in the domain of the actual function). Remember that [latex]y[/latex] is a length, so it can’t be negative, and [latex]y = 0[/latex] would mean there was no enclosure at all. So, it couldn’t have an area of 600 square feet.

Test [latex]y = 20[/latex] (here we chose the second derivative test): [latex]C''=\frac{16800}{y^3} \gt 0,[/latex] so this is a local minimum.

Since this is the only critical point in the domain, this must be the global minimum. Going back to our constraint function, we can find that when [latex]y = 20[/latex], [latex]x = 30.[/latex] The dimensions of the enclosure that minimize the cost are 20 feet by 30 feet.

Step 4. Look back at the question to make sure you answered what was asked.

The question asked us to find the dimensions of the least costly such enclosure. To that end, we

gave an answer of 20 feet x 30 feet, which represents the dimensions of a rectangle, [latex]\checkmark[/latex]
used the 2nd derivative to guarantee that these dimensions result in the minimum cost, [latex]\checkmark[/latex]
and used common sense to judge whether this answer makes sense in the context of the problem. [latex]\checkmark[/latex]

Maximizing Revenue

When trying to maximize their revenue, businesses also face the constraint of consumer demand. While a business would love to see lots of products at a very high price, typically demand decreases as the price of goods increases. In simple cases, we can construct that demand curve to allow us to maximize revenue.

EXAMPLE 2

Maximizing Revenue

A concert promoter has found that if she sells tickets for $50 each, she can sell 1200 tickets, but for each $5 she raises the price, 50 less people attend. What price should she sell the tickets at to maximize her revenue?

Show/Hide Solution

Solution

Step 1. Translate line by line into a picture, as in Figure 1, and math.

A picture doesn’t make sense for this problem. So, we’ll have to jump straight into translating the problem into math. We are trying to maximize revenue, and we know that [latex]R=pq[/latex], where [latex]p[/latex] is the price per ticket, and [latex]q[/latex] is the quantity of tickets sold.

The problem provides information about the demand relationship between price and quantity – as price increases, demand decreases. We need to find a formula for this relationship. To investigate, let’s calculate what will happen to attendance if we raise the price, organizing our thoughts in Table 1:

Price, [latex]p[/latex]

50

55

60

65

Quantity, [latex]q[/latex]

1200

1150

1100

1050

Table 1

You might recognize this as a linear relationship. We can find the slope for the relationship by using two points: [latex]m=\frac{1150-1200}{55-50}=\frac{-50}{5}=-10.[/latex]

You may notice that the second step in that calculation corresponds directly to the statement of the problem: the attendance drops 50 people for every $5 the price increases.

Using the point-slope form of the line, we can write the equation relating price and quantity: [latex]q-1200=-10(p-50).[/latex]

Simplifying to slope-intercept form gives the demand equation [latex]q=1700-10p.[/latex]

Substituting this into our revenue equation, we get an equation for revenue involving only one variable: [latex]R=pq=p(1700-10p)=1700p-10p^2.[/latex]

Step 2. Identify the objective function.

The “buzz” word in this problem that helps us identify the objective function is “maximize.” The problem asked us to “maximize revenue.” A maximum is something we know we can use calculus to find in Step 3. So,

[latex]\begin{array}{llll}R \hfill & = & pq & \\ R \hfill &= & p(1700-10p) \hfill & \\ R \hfill & = & 1700p-10{p}^{2} \hfill & \text{is our objective function of one variable.} \hfill \end{array}[/latex]

Step 3. Use calculus to find the optimum values.

Now, we can find the maximum of this function by finding critical numbers. [latex]R'=1700-20p[/latex], so [latex]R'=0[/latex] when [latex]p = 85[/latex].

Using the second derivative test, [latex]R''=-20 \lt 0[/latex] (for any value of [latex]p[/latex]), so the critical number is a local maximum. Since it is the only critical number, we can also conclude that it is the global maximum.

The promoter will be able to maximize revenue by charging $85 per ticket. At this price, she will sell [latex]q=1700-10(85)=850[/latex] tickets, generating $72,250 in revenue.

Step 4. Look back at the question to make sure you answered what was asked.

The question asked us to find the price that would maximize revenue. To that end, we

gave an answer of \$85, which represents a ticket’s sale price, [latex]\checkmark[/latex]
used the 2nd derivative to guarantee that this price results in the maximum revenue, [latex]\checkmark[/latex]
and used common sense to judge whether this answer makes sense in the context of the problem. [latex]\checkmark[/latex]

Marginal Revenue = Marginal Cost

You may have heard before that profit is maximized when marginal cost and marginal revenue are equal. Now you can see why people say that! (Even though it’s not completely true.)

Suppose we want to maximize profit. We know what to do – find the profit function, find its critical points, test them, etc.

But remember that Profit = Revenue – Cost. So Profit’ = Revenue’ – Cost’. That is, the derivative of the profit function is [latex]MR - MC[/latex].

Now let’s find the critical points – those will be where Profit’ = 0 or is undefined. Profit’ = 0 when [latex]MR - MC = 0[/latex], or where [latex]MR = MC[/latex].

Profit has critical points when Marginal Revenue and Marginal Cost are equal.

In all the cases we’ll see in this class, Profit will be very well behaved, and we won’t have to worry about looking for critical points where Profit’ is undefined. But remember that not all critical points are local maxs and mins! The places where [latex]MR = MC[/latex] could represent local maxs, local mins, or neither one!

EXAMPLE 3

Maximizing Profit

A company sells [latex]q[/latex] ribbon winders per year at [latex]\$p[/latex] per ribbon winder. The demand function for ribbon winders is given by: [latex]p=300-0.02q[/latex]. The ribbon winders cost $30 apiece to manufacture, plus there are fixed costs of $9000 per year. Find the quantity where profit is maximized.

Show/Hide Solution

Solution

Step 1. Translate line by line into a picture, as in Figure 1, and math.

A picture doesn’t make sense for this problem either. So, like Example 2, we’ll jump straight into translating the problem into math. We want to maximize profit, but there isn’t a formula for profit given. S o let’s make one.

We can find a function for Revenue = [latex]pq[/latex] using the demand function for [latex]p[/latex]. [latex]R(q)=(300-0.02q)q=300q-0.02q^2.[/latex]

We can also find a function for Cost, using the variable cost of $30 per ribbon winder, plus the fixed cost: [latex]C(q)=9000+30q.[/latex]

Putting them together, we get a function for Profit: [latex]P(q)=R(q)-C(q)=\left(300q-0.02q^2\right)-(9000+30q)=-0.02q^2+270q-9000[/latex]

Step 2. Identify the objective function.

The “buzz” word in this problem that helps us identify the objective function is “maximized.” The problem asked us to find where “profit is maximized.” A maximum is something we know we can use calculus to find in Step 3. So,

[latex]\begin{array}{llll} P(q) \hfill & = & R(q)-C(q) & \\ P(q) \hfill &= & \left(300q-0.02q^2\right)-(9000+30q) \hfill & \\ P(q) \hfill & = & -0.02q^2+270q-9000 \hfill & \text{is our objective function of one variable.} \hfill \end{array}[/latex]

Step 3. Use calculus to find the optimum values.

Now we have two choices. We can find the critical points of Profit by taking the derivative of [latex]P(q)[/latex] directly, or we can find [latex]MR[/latex] and [latex]MC[/latex] and set them equal. (Naturally, we’ll get the same answer either way.)

Let’s use [latex]MR = MC[/latex] this time.

[latex]\begin{align*} MR=& 300-0.04q\\ MC=& 30\\ 300-0.04q=& 30\\ 270=& 0.04q\\ q=& 6750 \end{align*}[/latex]

The only critical point is at [latex]q = 6750[/latex]. Now we need to be sure this is a local max and not a local min. In this case, we’ll look to the graph of [latex]P(q)[/latex] – it’s a downward opening parabola, so this must be a local max. And since it’s the only critical point, it must also be the global max.

Profit is maximized when they sell 6750 ribbon winders.

Step 4. Look back at the question to make sure you answered what was asked.

The question asked us to find the quantity that would maximize profit. To that end, we

gave an answer of 6750 ribbon winders, [latex]\checkmark[/latex]
used the graph of profit to verify that this is a maximum, [latex]\checkmark[/latex]
and used common sense to judge whether this answer makes sense in the context of the problem. [latex]\checkmark[/latex]

Section 3.5 Exercises

This content comes directly from OpenStax’s textbook Calculus, Volume 1 Section 4.7 Applied Optimization Problems.

Access this resource for free at https://openstax.org/books/calculus-volume-1/pages/4-7-applied-optimization-problems

[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]

Verbal

1. When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical points?

2. Why do you need to check the endpoints for optimization problems?

3. True or False. For every continuous nonlinear function, you can find the value [latex]x[/latex] that maximizes the function.

4. True or False. For every continuous nonconstant function on a closed, finite domain, there exists at least one [latex]x[/latex] that minimizes or maximizes the function.

Algebraic

For the following exercises, set up, but do not evaluate, each optimization problem.

5. You are the manager of an apartment complex with 50 units. When you set rent at $800/month, all apartments are rented. As you increase rent by $25/month, one fewer apartment is rented. Maintenance costs run $50/month for each occupied unit. What is the rent that maximizes the total amount of profit?

6. You are building five identical pens adjacent to each other with a total area of 1000m², as shown in Figure 2. What dimensions should you use to minimize the amount of fencing? A rectangle is divided into five sections, and each section has length [latex]y[/latex] and width [latex]x[/latex].

A rectangle is divided into five sections, and each section has length y and width x.

Figure 2

7. A window is composed of a semicircle placed on top of a rectangle, as in FIgure 3. If you have 20ft of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use [latex]r[/latex] to represent the radius of the semicircle.

A semicircular window is drawn with radius r.

Figure 3

8. You have a garden row of 20 watermelon plants that produce an average of 30 watermelons apiece. For any additional watermelon plants planted, the output per watermelon plant drops by one watermelon. How many extra watermelon plants should you plant?

9. You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs $5/ft²and the material for the sides costs $2/ft². You need a box with volume 4ft³. Find the dimensions of the box that minimize cost. Use [latex]x[/latex] to represent the length of the side of the box.

For the following exercises, use calculus to find the solution to each problem.

For 10-11, consider a limousine that gets [latex]m(v)=\frac{120−2v}{5}[/latex] mi/gal at speed [latex]v[/latex], the chauffeur costs $15/h, and gas is $3.5/gal.

10. Find the cost per mile at speed [latex]v[/latex].

11. Find the cheapest driving speed.

For 12-14, consider a pizzeria that sell pizzas for a revenue of [latex]R(x)=ax[/latex] and costs [latex]C(x)=b+cx+d{x}^{2}[/latex], where [latex]x[/latex] represents the number of pizzas.

12. Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?

13. Assume that [latex]R(x)=10x[/latex] and [latex]C(x)=2x+{x}^{2}[/latex]. How many pizzas sold maximizes the profit?

14. Assume that [latex]R(x)=15x[latex], and [latex]C(x)=60+3x+12{x}^{2}[/latex]. How many pizzas sold maximizes the profit?

For the following exercises, consider the construction of a pen to enclose an area.

15. You have 400ft of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?

16. You have 800ft of fencing to make a pen for hogs. If you have a river on one side of your property, what is the dimension of the rectangular pen that maximizes the area?

17. You need to construct a fence around an area of 1600ft². What are the dimensions of the rectangular pen to minimize the amount of material needed?

Answers to Section 3.5 Odd Problems

1. The critical points can be the minima, maxima, or neither.

3. False; [latex]y={x}^{2}[/latex] has a minimum only

5. [latex]P(x)=(50−x)(800+25x−50)[/latex]

7. [latex]A=20r−2{r}^{2}−\frac{1}{2}π{r}^{2}[/latex]

9. [latex]C(x)=5{x}^{2}+\frac{32}{x}[/latex] Differentiating, setting the derivative equal to zero and solving, we obtain [latex]x=\sqrt[3]{\frac{16}{5}}[/latex] and [latex]h=\sqrt[3]{\frac{25}{4}}[/latex]

11. approximately 34.02mph

13. 4

15. 100ft by100ft

17. 40ft by40ft

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Baylor University's Co-requisite Supplement for Calculus I Copyright © 2023 by Amy Graham Goodman is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

This content comes directly from Larry Musolino open textbook Techniques of Calculus 1 Section 4.5 Optimization Applications.

Access this resource for free at https://psu.pb.unizin.org/math110/chapter/4-5-optimization-applications/

Learning Objectives

Let’s Get Started Talking About Applied Optimization

Max/Min Applications

How To

Decode Max-Min Story Problems

EXAMPLE 1

Decoding Max-Min Story Problems

Solution

Maximizing Revenue

EXAMPLE 2

Maximizing Revenue

Solution

Marginal Revenue = Marginal Cost

EXAMPLE 3

Maximizing Profit

Solution

Section 3.5 Exercises

This content comes directly from OpenStax’s textbook Calculus, Volume 1 Section 4.7 Applied Optimization Problems.

Access this resource for free at https://openstax.org/books/calculus-volume-1/pages/4-7-applied-optimization-problems

Verbal

Algebraic

Answers to Section 3.5 Odd Problems

License

Share This Book