Section 3.2:  The Language of Graphs

Amy Graham Goodman

Section 3.2: The Language of Graphs

Learning Objectives

In this section, you will:

Describe a graph in terms of increasing/decreasing slopes.
Describe the rate of increasing/decreasing of the slope of a graph.
Articulate the two ways a graph can be concave up.
Articulate the two ways a graph can be concave down.
Describe what it means for a slope to have zero slope/concavity.
Sketch graphs with given increasing/decreasing/concavity conditions.

Let’s Get Started…

The key features of this section are applying language and notation to the slope of a graph AND to the slope-of-the-slope of a graph. When it comes to the slope of a graph, we are most interested in where the slope is positive, negative, or zero. These slopes indicate that the graph is increasing, decreasing, or neither. By contrast, the slope-of-the-slope of a graph tells us about the graph’s concavity. These features give us the relationships below.

The Slope of a Graph

The Slope of a Graph tells us that the graph is:

[latex]\begin{array} {lllll} \bullet \; \text{Increasing} & \Rightarrow & \text{Going up} \, \uparrow & \Rightarrow & \text{Positive slope} \\ \bullet \; \text{Decreasing} & \Rightarrow & \text{Going down} \, \downarrow & \Rightarrow & \text{Negative slope} \\ \bullet \; \text{Zero} & \Rightarrow & \text{Horizontal} \, \leftrightarrow & \Rightarrow & \text{Flat} \end{array}[/latex]

Note that the Intervals we use to describe these features are always with respect to [latex]x-[/latex]values.

EXAMPLE 1

Describing Increasing/Decreasing with Interval Notation

What are the intervals of increasing and decreasing for the graph in Figure 1?

Figure 1

Show/Hide Solution

Solution

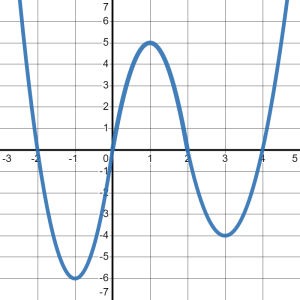
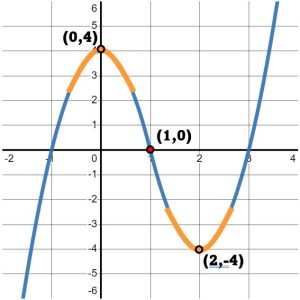
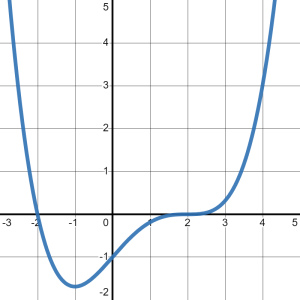
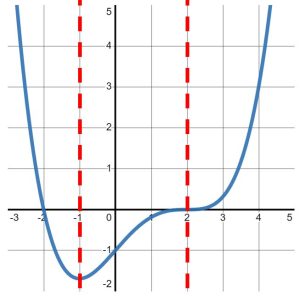
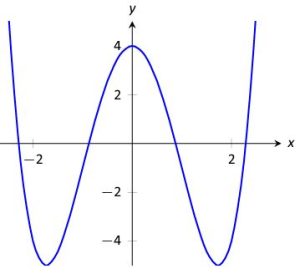
The key for questions like this is to focus on the SLOPES of the graph, NOT the [latex]y-[/latex]values of the graph. Then, we will write down what we observe as we read the graph from left to right. For example, when I trace the graph with my finger from the bottom-left corner, I immediately begin to move UP and to the right, as seen in Figure 2.

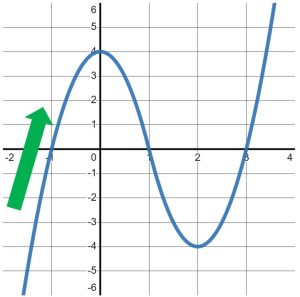
Figure 2

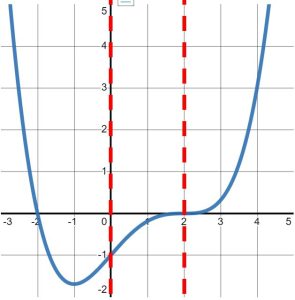
When does the graph stop moving up? It stops moving up precisely at the point where it changes direction again. Note that after the point [latex]\left(0,4\right)[/latex], the graph begins to move DOWN, as in Figure 3.

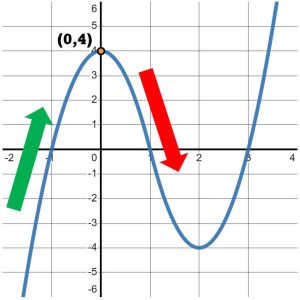
Figure 3

So, we can definitely say that this graph increases from where it starts to the point [latex]\left(0,4\right)[/latex]. We write that with respect to the [latex]x-[/latex]values of this interval. Since the problem did not specify a starting value, we will assume this graph starts on the far-left of the number line, that is at [latex]-\infty[/latex]. This first interval of increasing ends when the [latex]x-[/latex]value is [latex]0[/latex]. So, we write the interval of increasing as:

[latex]\left(-\infty,0\right)[/latex].

Note that we used soft parentheses for this interval – not hard brackets. That is because NEITHER [latex]-\infty[/latex] nor [latex]0[/latex] are included in the interval.

The graph cannot be increasing at [latex]x=-\infty[/latex] because [latex]x[/latex] can never equal [latex]-\infty[/latex]. [latex]-\infty[/latex] is not a value.
The graph cannot be increasing at [latex]x=0[/latex] because that is the point where the graph changes direction. The slope of the graph is not positive at [latex]x=0[/latex].

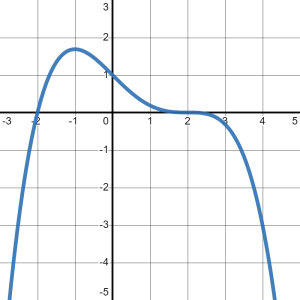
Continuing to trace the graph, we see that it continues down until the point [latex]\left(2,-4\right)[/latex]. After that point, we start tracing up again, as in Figure 4.

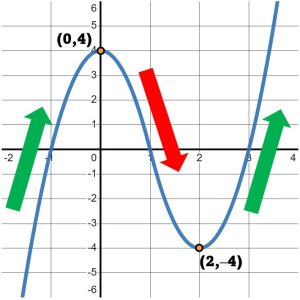
Figure 4

So, we can definitely say that the graph decreases from the point [latex]\left(0,4\right)[/latex] to the point [latex]\left(2,-4\right)[/latex]. As before, we will write that interval of decreasing with respect to the [latex]x-[/latex]values:

[latex]\left(0,2\right)[/latex].

Again, notice that we used soft parentheses for both ends of this interval.

As the graph was not increasing at the point [latex]\left(0,4\right)[/latex], it is also not decreasing there. [latex]\left(0,4\right)[/latex] is the instance where the graph transitions from increasing to decreasing – or positive slopes to negative slopes.
Likewise, the graph is not decreasing at [latex]\left(2,-4\right)[/latex]. [latex]\left(2,-4\right)[/latex] is the point where the slope of the graph changes direction again.

In fact, we observed that after the point [latex]\left(2,-4\right)[/latex], the graph increases. Since we do not see another place where the graph changes direction, we will assume is continues to increases forever, that is to [latex]\infty[/latex]. Therefore, we write our second interval of increasing as:

[latex]\left(2,\infty\right)[/latex].

When we write our complete answer all together, we could denote the fact that there were two intervals of increasing by using the union symbol [latex]\cup[/latex] between them. Thus, our final answer would read:

[latex]\textcolor{blue}{\begin{array}{ll} \text{The graph is increasing on} & \left(-\infty,0\right) \, \cup \, \left(2,\infty\right) \hfill \\ \text{The graph is decreasing on} & \left(0,2\right). \hfill \end{array}}[/latex]

Note that we observed the graph was neither increasing nor decreasing at [latex]\left(0,4\right)[/latex] and [latex]\left(2,-4\right)[/latex]. At these two points, the graph has zero slope. In fact, because the graph increases to [latex]\left(0,4\right)[/latex] and decreases away, we can say that:

the graph has a local maximum at [latex]\left(0,4\right)[/latex].

Similarly, because the graph decreases to [latex]\left(2,-4\right)[/latex] and increases away, we can say that:

the graph has a local minimum at [latex]\left(2,-4\right)[/latex].

EXAMPLE 2

Describing Increasing/Decreasing with Interval Notation

What are the intervals of increasing and decreasing for the graph in Figure 5?

Figure 5

Show/Hide Solution

Solution

Since we saw in Example 1 that the transition points are where the graph changes direction, let’s focus on those first. Reading this graph from left to right, we can see the graph changes direction at the points [latex]\left(-1,-6\right), \, \left(1,5\right), \, \text{and} \, \left(3,-4\right)[/latex]. If we put together the observations we made in Example 1, we can use those points to break up the [latex]x-[/latex]axis into subintervals, as in Figure 6.

Figure 6

Now we can tackle the graph one subinterval at a time. Let’s start with Subinterval #1. As we read from left to right, note that the graph is decreasing from the upper-left of the picture to the point [latex]\left(-1,-6\right)[/latex]. Focusing on the [latex]x-[/latex]values, we’ll assume the graph comes from the far-left of the [latex]x-[/latex]axis and say that this graph is decreasing on the interval [latex]\left(-\infty,-1\right)[/latex].

Looking at Subinterval #2, observe that the graph increases from the point [latex]\left(-1,-6\right)[/latex] to the point [latex]\left(1,5\right)[/latex]. Using the [latex]x-[/latex]values to denote that, we’ll say that this graph is increasing on the interval [latex]\left(-1,1\right)[/latex].

In Subinterval #3, we can see the graph decreases again to the point [latex]\left(3,-4\right)[/latex]. Since this subinterval starts at the point [latex]\left(1,5\right)[/latex], we can use the [latex]x-[/latex]values of these points to record this interval of decreasing as [latex]\left(1,3\right)[/latex].

Finally, in Subinterval #4, the graph begins to increase again, and we never see another instance of it changing direction. So, we can say this graph increases from the point [latex]\left(3,-4\right)[/latex] to the far-right of the [latex]x-[/latex]axis, or, more precisely, increases on the interval [latex]\left(3,\infty\right)[/latex].

Putting all these observations together, we can write our final answer more concisely as:

[latex]\textcolor{blue}{\begin{array}{ll} \text{The graph is decreasing on} \hfill & \left(-\infty,-1\right) \, \cup \, \left(1,3\right) \hfill \\ \text{The graph is increasing on} \hfill & \left(-1,1\right) \, \cup \, \left(3,\infty\right). \hfill \end{array}}[/latex]

Note again that, through this process of identifying intervals of increasing and decreasing, we have identified local minimums at [latex]\left(-1,6\right)[/latex] and [latex]\left(3,-4\right)[/latex] and a local maximum at [latex]\left(1,5\right)[/latex].

Try It #1

What are the intervals of increasing and decreasing for the graph in Figure 7?

Figure 7

EXAMPLE 3

Sketching a Graph Given Intervals of Increasing/Decreasing

Sketch a possible graph of a curve where:

[latex]\begin{array}{ll} \text{The graph is increasing on} \hfill & \left(-\infty,-4\right) \, \cup \, \left(-1,2\right) \hfill \\ \text{The graph is decreasing on} \hfill & \left(-4,-1\right) \, \cup \, \left(2,\infty\right). \hfill \end{array}[/latex]

Show/Hide Solution

Solution

Imagine the shape of the graph on a number line, as in Figure 8. This visual helps us think about how the 4 subintervals of the graph could fit together into a cohesive whole.

Figure 8

Looking at Figure 8, we can imagine an “up-down-up-down” pattern to the graph. We can also see that where the subintervals transition from increasing to decreasing or vice versa we have potential for maximum/minimum points. For example, this graph will have a local maximum at [latex]x=-4[/latex], a local minimum at [latex]x=-1[/latex], and another local maximum at [latex]x=2[/latex]. Therefore, one possible version of this graph might be Figure 9.

Figure 9

The absence of a scale on the [latex]y-[/latex]axis on this graph is deliberate. The height of each maximum and depth of the minimum is arbitrary. The coordinates of these maximums could be [latex]\left(-4,250\right)[/latex] and [latex]\left(2,150\right)[/latex] or [latex]\left(-4,0.25\right)[/latex] and [latex]\left(2,0.15\right)[/latex]. A similar argument could be made for the coordinates of the minimum at [latex]x=-1[/latex].

It is also arbitrary which maximum is higher. Maybe the [latex]y-[/latex]value at [latex]x=2[/latex] is higher than the [latex]y-[/latex]value at [latex]x=-4[/latex]. That would be another correct possibility. Or, the [latex]y-[/latex]values of the maximums could be equal.

What is not arbitrary is the overall “M” shape of the graph. Regardless of the [latex]y-[/latex]values we choose for any of the points, all possible graphs for these given intervals will have a similar “up to [latex]x=-4[/latex], down to [latex]x=-1[/latex], up to [latex]x=2[/latex], down forever after” pattern. Anything that meets those criteria is a correct possible graph.

Try It #2

Sketch a possible graph of a curve where:

[latex]\begin{array}{ll} \text{The graph is decreasing on} \hfill & \left(-\infty,-4\right) \, \cup \, \left(-1,2\right) \hfill \\ \text{The graph is increasing on} \hfill & \left(-4,-1\right) \, \cup \, \left(2,\infty\right). \hfill \end{array}[/latex]

The Slope-of-the-Slope of a Graph

The Slope-of-the-Slope a Graph tells us that the graph is:

[latex]\begin{array} {lllll} \bullet \; \text{Concave Up} & \Rightarrow & \text{Graph smiles} \, \cup & \Rightarrow & \text{Slope increasing} \\ \bullet \; \text{Concave Down} & \Rightarrow & \text{Graph frowns} \, \cap & \Rightarrow & \text{Slope decreasing} \\ \bullet \; \text{Zero} & \Rightarrow & \text{Neither} & \Rightarrow & \text{No concavity} \end{array}[/latex]

Note that, here too, the Intervals we use to describe these features are always with respect to [latex]x-[/latex]values.

EXAMPLE 4

Describing Concavity with Interval Notation

What are the intervals of concavity for the graph in Example 1’s Figure 1?

Figure 1 from Example 1

Show/Hide Solution

Solution

This time, we are making observations about where the graph smiles and frowns. Notice that, as we read this graph from left to right, the graph begins frowning, as seen in Figure 10.

Figure 10

So, the first thing we see is a frown. Where does it start? Where does it stop? Since this graph doesn’t have any other smiling/frowning features as we start reading from the left, we may assume this frown – or interval where the graph is concave down – begins at [latex]-\infty[/latex]. Where does the frown end? Maybe it doesn’t. We would know for sure that the concave down part of the graph ends if we could also see a concave up – smiling – part of the graph. If we keep reading from left to right, we’ll note that the graph does have an interval where it is smiling – or concave up – as highlighted in Figure 11.

Figure 11

We already know from Example 1 that this graph has a local maximum at the point [latex]\left(0,4\right)[/latex]. Note that this appears to be the peak of the concave down interval (frown). We also know from Example 1 that this graph has a local minimum at the point [latex]\left(2,-4\right)[/latex]. That point also appears to be the bottom of the concave up – smiling – interval. The graph changes from concave down to concave up somewhere between [latex]\left(0,4\right)[/latex] and [latex]\left(2,-4\right)[/latex]. Calculus would tell us precisely where, but the change often (though not always) happens halfway between extreme values. Halfway between [latex]x=0[/latex] and [latex]x=2[/latex] would make [latex]x=1[/latex] a good guess. Does that appear reasonable when we look at the graph? The point [latex]\left(1,0\right)[/latex] is highlighted in Figure 12.

Figure 12

Visually, [latex]x=1[/latex] looks like it is the transition point where concave down (frowning) ends and concave up (smiling) begins. Therefore, we can say the graph is concave down on the interval:

[latex]\textcolor{blue}{\left(-\infty,1\right)}[/latex].

[latex]x=1[/latex] will also be where the concave up interval starts. Where does it end? If we keep reading from [latex]x=1[/latex] to the right, it looks like the graph keeps on smiling. There are no other frowning/smiling features. Therefore, we can assume the graph is concave up to the far-right of the [latex]x-[/latex] axis, or [latex]\infty[/latex]. Thus, we can write the interval where the graph is concave up as

[latex]\textcolor{blue}{\left(1,\infty\right)}[/latex].

Note that we, again, used soft-parentheses for these intervals. This notation excludes [latex]x=1[/latex] from both intervals. Why? For the same reason the transition points in Examples 1 and 2 were excluded. The graph cannot have either – or both – features (concave up and concave down) at the point where it transitions. There is no concavity at [latex]x=1[/latex]. In fact, we call the point [latex]\left(1,0\right)[/latex] an inflection point.

EXAMPLE 5

Describing Concavity with Interval Notation

What are the intervals of concavity for the graph in Example 2’s Figure 5?

Figure 5 from Example 2

Show/Hide Solution

Solution

Combining our knowledge from both Example 3 and Example 2, we know to read the graph and look for instances of smiling/frowning. Also, we know that this graph has local minimums at [latex]\left(-1,-6\right)[/latex] and [latex]\left(3,-4\right)[/latex] and a local maximum at [latex]\left(1,5\right)[/latex]. These extreme points are good places to look for easily identifiable indicators of concavity. Accordingly, we can see that the graph is concave up (smiling) at each minimum and concave down (frowning) at each maximum, as in Figure 13.

Figure 13

These observations give us a general “concave up, concave down, concave up” pattern for this graph. Since concave up is the first feature we see, we may assume that its interval starts at [latex]-\infty[/latex]. Where does it end? Where does the concave down interval we see at [latex]\left(1,5\right)[/latex] begin? Since the lowest point of the concave up interval is the minimum point [latex]\left(-1,-6\right)[/latex], and the highest point of the concave down interval is the maximum point [latex]\left(1,5\right)[/latex], we may assume the transition happens between these points at [latex]x=0[/latex]. This means that the first concave up interval is [latex]\left(-\infty,0\right)[/latex].

Identifying [latex]x=0[/latex] as a transition point also means that this is where the concave down interval begins. Where does it end? It definitely ends somewhere after the peak at [latex]\left(1,5\right)[/latex] and before the concave up’s minimum point at [latex]\left(3,-4\right)[/latex]. These observations point to a transition point – a point of inflection – at [latex]x=2[/latex]. This means the concave down interval for this graph is [latex]\left(0,2\right)[/latex].

Since there is only one interval of concavity remaining, and we know it starts at [latex]x=2[/latex], we can say the second concave up interval for this graph is [latex]\left(2,\infty\right)[/latex].

Putting all these observations together, we can write our final answer more concisely as:

[latex]\textcolor{blue}{\begin{array}{ll} \text{The graph is concave up on} \hfill & \left(-\infty,0\right) \, \cup \, \left(2,\infty\right) \hfill \\ \text{The graph is concave down on} \hfill & \left(0,2\right). \hfill \end{array}}[/latex]

We have also identified two points of inflection at [latex]\left(0,0\right)[/latex] and [latex]\left(2,0\right)[/latex], as seen in Figure 14.

Figure 14

Try It #3

What are the intervals of increasing and decreasing for the graph in Try It #1’s Figure 7?

Figure 7 from Try It #1

EXAMPLE 6

Sketching a Graph Given Intervals of Concavity

Sketch a possible graph of a curve where:

[latex]\begin{array}{ll} \text{The graph is concave up on} \hfill & \left(-\infty,-5\right) \, \cup \, \left(-1,3\right) \hfill \\ \text{The graph is concave down on} \hfill & \left(-5,-1\right) \, \cup \, \left(3,\infty\right). \hfill \end{array}[/latex]

Show/Hide Solution

Solution

Like we did in Example 3, let’s imagine the shape of the graph on a number line, as in Figure 15. This visual, again, helps us think about how the 4 subintervals of the graph could fit together into a cohesive whole.

Figure 15

Looking at Figure 15, we can imagine a “smile-frown-smile-frown” pattern to the graph. We can also see that where the subintervals transition from concave up to concave down or vice versa we have potential for points of inflection. Therefore, one possible version of this graph might be Figure 16.

Figure 16

Like in Example 3, the absence of a scale on the [latex]y-[/latex]axis on this graph is deliberate. The [latex]y-[/latex]values of the points of inflection are arbitrary. In Figure 16, we sketched a graph where all the points of inflection had the same [latex]y-[/latex]value. However, any sketch that included the “smile to [latex]x=-5[/latex], frown to [latex]x=-1[/latex], smile to [latex]x=3[/latex], frown forever after” pattern would be a correct possible graph for the given criteria.

Try It #4

Sketch a possible graph of a curve where:

[latex]\begin{array}{ll} \text{The graph is concave down on} \hfill & \left(-\infty,-5\right) \, \cup \, \left(-1,3\right) \hfill \\ \text{The graph is concave up on} \hfill & \left(-5,-1\right) \, \cup \, \left(3,\infty\right). \hfill \end{array}[/latex]

Putting It All Together

So far, we have handled the concepts of increasing/decreasing and concave up/down separately, However, we are usually concerned with all of these features for a given graph.

EXAMPLE 7

Describing Increasing/Decreasing and Concavity with Interval Notation

What are the intervals of increasing, decreasing, and concavity for the graph Figure 17?

Figure 17

Show/Hide Solution

Solution

Let’s begin with the same strategy we used in Example 2 to identify intervals of increasing and decreasing. That is, let’s use possible extreme values to divide the graph into subintervals, as in Figure 18.

Figure 18

If we focus just on the pattern of increasing/decreasing in Figure 18, we can see that we decrease to [latex]x=-1[/latex] and increase to [latex]x=2[/latex]. However, the graph doesn’t change direction at [latex]x=2[/latex] and turn to decrease again. It keeps increasing. So, what’s happening at [latex]x=2[/latex]? Does the graph just keep increasing forever after [latex]x=-1[/latex]?

Those a good questions. The answers depend on the behavior of the graph at [latex]x=2[/latex]. What’s happening there? Does the graph cross the [latex]x-[/latex]axis at [latex]x=2[/latex] like a linear graph? No. As the graph approaches [latex]x=2[/latex], it flattens out. In fact, it would have a perfectly flat tangent line at [latex]x=2[/latex]. This means the graph has [latex]0[/latex] slope at [latex]x=2[/latex]. The graph is neither increasing nor decreasing at that point. That’s important to note because it means we have to exclude [latex]x=2[/latex] from any intervals of increasing/decreasing.

Since the graph never changes direction again after [latex]x=2[/latex], we can say:

[latex]\textcolor{blue}{\begin{array}{ll} \text{The graph is decreasing on} \hfill & \left(-\infty,-1\right) \hfill \\ \text{The graph is increasing on} \hfill & \left(-1,2\right) \, \cup \, \left(2,\infty\right). \hfill \end{array}}[/latex]

Now, if we change our focus on Figure 17 to intervals of concavity, we can still divide the graph into subintervals. This time, we will look for where the graph changes from concave up to down or vice versa, as in Figure 19.

Figure 19

Looking at just the pattern of “smiling and frowning” in Figure 19, we can see that the graph starts off smiling. In fact, it looks like it smiles until about [latex]x=0[/latex], where it changes to a frown. The graph only completes the left-side of a frown until at [latex]x=2[/latex] a smile begins. Therefore, we can say:

[latex]\textcolor{blue}{\begin{array}{ll} \text{The graph is concave up on} \hfill & \left(-\infty,0\right) \, \cup \, \left(2,\infty\right) \hfill \\ \text{The graph is concave down on} \hfill& \left(0,2\right). \hfill \end{array}}[/latex]

Try It #5

What are the intervals of increasing, decreasing, and concavity for the graph Figure 20?

Figure 20

EXAMPLE 8

Sketching a Graph Given Intervals of Increasing, Decreasing, & Concavity

Sketch a possible graph of a curve where:

[latex]\begin{array}{ll} \text{The graph is increasing on} \hfill & \left(-\infty,-3\right) \, \cup \, \left(3,\infty\right) \hfill \\ \text{The graph is decreasing on} \hfill & \left(-3,0\right) \, \cup \, \left(0,3\right). \hfill \\ \text{The graph is concave down on} \hfill & \left(-\infty,-2\right) \, \cup \, \left(0,2\right). \hfill \\ \text{The graph is concave up on} \hfill & \left(-2,0\right) \, \cup \, \left(2,\infty\right). \hfill \end{array}[/latex]

Show/Hide Solution

Solution

Make a number line for just the intervals of increasing and decreasing. You should have an “up-down-down-up” pattern. Then, make a number line for the intervals of concavity. You should have a “frown-smile-frown-smile” pattern.

Begin with a rough sketch of the intervals of increasing and decreasing. Now, begin to bend the curve according to the pattern of concavity. One possible sketch could be a graph like the one in Figure 21.

Figure 21

Remember, the [latex]y-[/latex]values are arbitrary. The shape of the graph is what is most important.

Section 3.2 Exercises

This content comes directly from Gregory Hartman’s Open APEX Calculus: University of North Dakota Edition Section 3.3: Increasing and Decreasing Functions and Section 3.4 Concavity and the Second Derivative.

[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]

1. In your own words describe what it means for a function to be increasing.

2. What does a decreasing function “look like”?

3. Sketch a graph of a function on [0, 2] that is increasing.

4. Give an example of a function describing a situation where it is “bad” to be increasing and “good” to be decreasing.

For the following, identify the intervals of increasing and decreasing.

5.

6.

7. Sketch a graph of a function that is concave up on [latex]\left(0,1\right)[/latex] and concave down on [latex]\left(1,2\right)[/latex]

8. Sketch a graph of a function that is

Increasing and concave up on [latex]\left(0,1\right)[/latex]
Increasing and concave down on [latex]\left(1,2\right)[/latex]
decreasing and concave down on [latex]\left(2,3\right)[/latex]
increasing and concave down on [latex]\left(3,4\right)[/latex]

9. Is it possible for a function to be increasing and concave down on [latex]\left(0,\infty\right)[/latex] with a horizontal asymptote at [latex]y=1[/latex]? If so, give a sketch of such a function.

10. Is it possible for a function to be increasing and concave up on [latex]\left(0,\infty\right)[/latex] with a horizontal asymptote at [latex]y=1[/latex]? If so, give a sketch of such a function.

11. Given the graph of [latex]f[/latex] identify the concavity of [latex]f[/latex]and its inflection points.

Answers to Section 3.2 Odd Problems

1. Answers will vary. Generally, the function rises from left to right.

3. Answers will vary.

[latex]\begin{array}{lll} 5. \hfill & \text{The graph is increasing on} \hfill & \left(0,\frac{\pi}{6}\right) \, \cup \, \left(\frac{\pi}{2},\frac{5\pi}{6}\right) \, \cup \, \left(\frac{3\pi}{2},2\pi\right) \hfill \\ & \text{The graph is decreasing on} \hfill & \left(\frac{\pi}{6},\frac{\pi}{2}\right) \, \cup \, \left(\frac{5\pi}{6},\frac{3\pi}{2}\right). \hfill \end{array}[/latex]

7. Answers will vary

9. Yes. Answers will vary.

[latex]\begin{array}{lll} 7. \hfill & \text{The graph is concave up on} \hfill & \left(-\infty,-1\right) \, \cup \, \left(1,\infty\right) \hfill \\ & \text{The graph is concave down on} \hfill & \left(-1,1\right) \hfill \\ & \text{The inflection points occur when} \hfill & x=-1 \, \text{and} \, x=1. \hfill \end{array}[/latex]

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Baylor University's Co-requisite Supplement for Calculus I Copyright © 2023 by Amy Graham Goodman is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Learning Objectives

Let’s Get Started…

The Slope of a Graph

EXAMPLE 1

Describing Increasing/Decreasing with Interval Notation

Solution

EXAMPLE 2

Describing Increasing/Decreasing with Interval Notation

Solution

Try It #1

EXAMPLE 3

Sketching a Graph Given Intervals of Increasing/Decreasing

Solution

Try It #2

The Slope-of-the-Slope of a Graph

EXAMPLE 4

Describing Concavity with Interval Notation

Solution

EXAMPLE 5

Describing Concavity with Interval Notation

Solution

Try It #3

EXAMPLE 6

Sketching a Graph Given Intervals of Concavity

Solution

Try It #4

Putting It All Together

EXAMPLE 7

Describing Increasing/Decreasing and Concavity with Interval Notation

Solution

Try It #5

EXAMPLE 8

Sketching a Graph Given Intervals of Increasing, Decreasing, & Concavity

Solution

Section 3.2 Exercises

This content comes directly from Gregory Hartman’s Open APEX Calculus: University of North Dakota Edition Section 3.3: Increasing and Decreasing Functions and Section 3.4 Concavity and the Second Derivative.

Answers to Section 3.2 Odd Problems

License

Share This Book