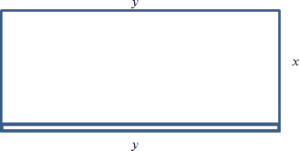Step 1. Translate line by line into a picture, as in Figure 1, and math.
Figure 1
Let's use the variable names from our picture to translate the words from the problem into equations. So, [latex]x[/latex] and [latex]y[/latex] will be the dimensions of the enclosure, with [latex]y[/latex] being the length of the side made of blocks. Then: [latex]\text{Area} = A = xy = 600.[/latex]
[latex]2x + y[/latex] costs $7 per foot, [latex]y[/latex] costs $14 per foot, so
[latex]\text{Cost} = C = 7(2x + y) + 14y = 14x + 21y.[/latex]
Step 2. Identify the objective function.
The "buzz" word in this problem that helps us identify the objective function is "least." The problem asked for the "least costly enclosure." That means, we want to find [latex]x[/latex] and [latex]y[/latex] so that [latex]C[/latex] is minimized. A minimum is something we know we can use calculus to find in Step 3. So,
[latex]\begin{array}{cc}\hfill C = 7(2x + y) + 14y = 14x + 21y \hfill & \hfill \text{is our objective function.} \hfill \end{array}[/latex]
As it stands, though, this objective function has two variables. So, we need to use the constraint equation. The constraint equation is the fixed area [latex]A = xy = 600[/latex]. Solve [latex]A[/latex] for [latex]x[/latex] to get [latex]x=\frac{600}{y}[/latex], and then substitute into [latex]C[/latex] to get an objective function of one variable.
[latex]\begin{array}{llll}C \hfill &= & 14\left(\frac{600}{y}\right)+21y \hfill & \\ C\hfill & = & \frac{8400}{y}+21y \hfill & \text{is our objective function of one variable.} \hfill \end{array}[/latex]
Step 3. Use calculus to find the optimum values.
Now that we have a function of just one variable, we can find the minimum using calculus.
[latex]C'=-\frac{8400}{y^2}+21[/latex]
[latex]C'[/latex] is undefined for [latex]y = 0[/latex], and [latex]C' = 0[/latex] when [latex]y = 20[/latex] or [latex]y = -20[/latex].
Of these three critical numbers, only [latex]y = 20[/latex] makes sense (is in the domain of the actual function). Remember that [latex]y[/latex] is a length, so it can’t be negative, and [latex]y = 0[/latex] would mean there was no enclosure at all. So, it couldn't have an area of 600 square feet.
Test [latex]y = 20[/latex] (here we chose the second derivative test): [latex]C''=\frac{16800}{y^3} \gt 0,[/latex] so this is a local minimum.
Since this is the only critical point in the domain, this must be the global minimum. Going back to our constraint function, we can find that when [latex]y = 20[/latex], [latex]x = 30.[/latex] The dimensions of the enclosure that minimize the cost are 20 feet by 30 feet.