Section 4.3: Describing Area Over an Interval
Learning Objectives
In this section, you will:
- Recognize the geometric shape created by the graph of a function and the x-axis.
- Describe the area of a geometric shape that is defined by a function’s graph and another dimension that can vary.
Let's Get Started...
Start thinking about finding areas with geometry with The Organic Chemistry Tutor's Intro:
Then get more symbolic with this video on YouTube by James Hamblin:
Section 4.3 Exercises
This content comes directly from Matthew Boelkins' open textbook Active Calculus Section 5.1 Constructing Accurate Graphs of Antiderivatives.
Access this resource for free at https://activecalculus.org/single/sec-5-1-antid-graphs.html
[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]
1. Figure 1 below shows the graph of [latex]f[/latex].

Figure 1
If [latex]F'=f[/latex] and [latex]F\left(0\right)=0[/latex], find [latex]F\left(b\right)[/latex] for [latex]b=1, 2, 3, 4, 5, 6[/latex] and fill these values in the following table.
| [latex]b[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] |
| [latex]F\left(b\right)[/latex] |
2. Consider the piecewise linear function [latex]f[/latex] given in Figure 2. Let the functions [latex]A, B,[/latex] and [latex]C[/latex] be defined by the rules
[latex]A\left(x\right)=\int_{-1}^{x} f\left(t\right) \,dt, \;\; B\left(x\right)=\int_{0}^{x} f\left(t\right) \,dt, \;\;[/latex]and[latex]\;\;C\left(x\right)=\int_{1}^{x} f\left(t\right) \,dt.[/latex]
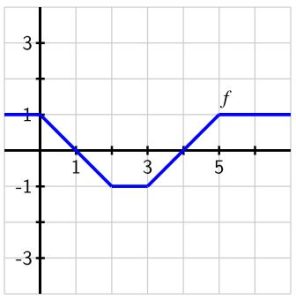
Figure 2
a. For the values [latex]x=-1, 0, 1, 2, 3, 4, 5, 6[/latex] make a table that lists corresponding values of [latex]A\left(x\right), B\left(x\right),[/latex] and [latex]C\left(x\right)[/latex].
b. Sketch graphs of [latex]A, B,[/latex] and [latex]C[/latex].
c. How are the graphs of [latex]A, B,[/latex] and [latex]C[/latex] related?
d. How would you best describe the relationship between the function [latex]A[/latex] and the function [latex]f[/latex]?
Answers to Section 4.3 Problems
1.
| [latex]b[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] |
| [latex]F\left(b\right)[/latex] | -1 | -2 | -2.5 | -2 | -1 | -0.5 |
2. a.
| [latex]x[/latex] | [latex]-1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] | [latex]4[/latex] | [latex]5[/latex] | [latex]6[/latex] |
| [latex]A\left(x\right)[/latex] | 0 | 1 | 1.5 | 1 | 0 | -0.5 | 0 | 1 |
| [latex]B\left(x\right)[/latex] | -1 | 0 | 0.5 | 0 | -1 | -1.5 | -1 | 0 |
| [latex]C\left(x\right)[/latex] | -1.5 | -0.5 | 0 | -0.5 | -1.5 | -2 | -1.5 | -0.5 |
Note that [latex]A\left(x\right)=1+B\left(x\right)[/latex] and [latex]C\left(x\right)=B\left(x\right)-0.5[/latex].
b. See Figure 3
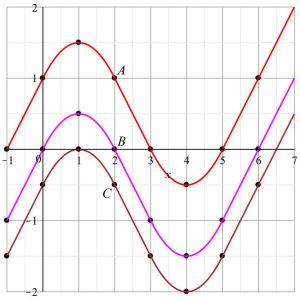
Figure 3
c. [latex]A, B,[/latex] and [latex]C[/latex] are vertical translations of each other.
d. [latex]A'=f[/latex]
