Section 1.1: Power Functions and Polynomials
Section 1.1 Part 1: Power Functions and Polynomials
(Part 2 follows regarding Graphs of Polynomial Functions.)
This content comes directly from OpenStax's textbook Algebra and Trigonometry Section 5.2 Power Functions and Polynomial Functions.
Learning Objectives
In this section, you will:
- Identify power functions.
- Identify end behavior of power functions.
- Identify polynomial functions.
- Identify the degree and leading coefficient of polynomial functions.
Let's Get Started...

Figure 1 (credit: Jason Bay, Flickr)
Suppose a certain species of bird thrives on a small island. Its population over the last few years is shown in Table 1.
| Year |
|
|
|
|
|
| Bird Population |
|
|
|
|
|
Table 1
The population can be estimated using the function[latex]\,P\left(t\right)=-0.3{t}^{3}+97t+800,\,[/latex]where[latex]\,P\left(t\right)\,[/latex]represents the bird population on the island[latex]\,t\,[/latex]years after 2009. We can use this model to estimate the maximum bird population and when it will occur. We can also use this model to predict when the bird population will disappear from the island. In this section, we will examine functions that we can use to estimate and predict these types of changes.
Identifying Power Functions
Before we can understand the bird problem, it will be helpful to understand a different type of function. A power function is a function with a single term that is the product of a real number, a coefficient, and a variable raised to a fixed real number.
As an example, consider functions for area or volume. The function for the area of a circle with radius r is
and the function for the volume of a sphere with radius r is
Both of these are examples of power functions because they consist of a coefficient,[latex]\,\pi \,[/latex]or[latex]\,\frac{4}{3}\pi ,\,[/latex]multiplied by a variable[latex]\,r\,[/latex]raised to a power.
Power Function
A power function is a function that can be represented in the form
[latex]f\left(x\right)=k{x}^{p}[/latex]
where[latex]\,k\,[/latex] and[latex]\,p\,[/latex]are real numbers, and[latex]\,k\,[/latex]is known as the coefficient.
 Q&A
Q&A
Is[latex]\,f\left(x\right)={2}^{x}\,[/latex]a power function?
No. A power function contains a variable base raised to a fixed power. This function has a constant base raised to a variable power. This is called an exponential function, not a power function.
EXAMPLE 1
Identifying Power Functions
Which of the following functions are power functions?
Show/Hide Solution
 Solution
Solution
All of the listed functions are power functions.
The constant and identity functions are power functions because they can be written as[latex]\,f\left(x\right)={x}^{0}\,[/latex]and[latex]\,f\left(x\right)={x}^{1}\,[/latex]respectively.
The quadratic and cubic functions are power functions with whole number powers[latex]\,f\left(x\right)={x}^{2}\,[/latex]and[latex]\,f\left(x\right)={x}^{3}.[/latex]
The reciprocal and reciprocal squared functions are power functions with negative whole number powers because they can be written as[latex]\,f\left(x\right)={x}^{-1}\,[/latex]and[latex]\,f\left(x\right)={x}^{-2}.[/latex]
The square and cube root functions are power functions with fractional powers because they can be written as[latex]\,f\left(x\right)={x}^{\frac{1}{2}}\,[/latex]or[latex]\,f\left(x\right)={x}^{\frac{1}{3}}.[/latex]
 Try It #1
Try It #1
Which functions are power functions?
[latex]\begin{array}{ccc}\hfill f\left(x\right)& =& 2x\cdot 4{x}^{3}\hfill \\ \hfill g\left(x\right)& =& -{x}^{5}+5{x}^{3}\hfill \\ \hfill h\left(x\right)& =& \frac{2{x}^{5}-1}{3{x}^{2}+4}\hfill \end{array}[/latex]
Identifying End Behavior of Power Functions
Figure 2 shows the graphs of[latex]\,f\left(x\right)={x}^{2},\,g\left(x\right)={x}^{4},[/latex] and [latex]h\left(x\right)={x}^{6},[/latex] which are all power functions with even, whole-number powers. Notice that these graphs have similar shapes. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.
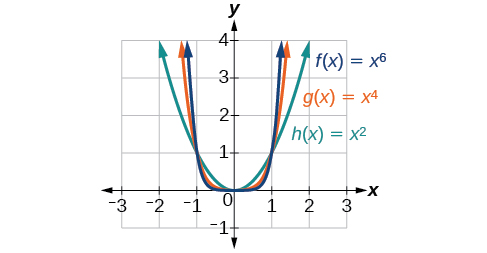
Figure 2 Even-power functions
To describe the behavior as numbers become larger and larger, we use the idea of infinity. We use the symbol[latex]\,\infty \,[/latex]for positive infinity and[latex]\,\mathrm{-\infty }\,[/latex]for negative infinity. When we say that “[latex]x\,[/latex]approaches infinity,” which can be symbolically written as[latex]\,x\to \infty ,\,[/latex]we are describing a behavior; we are saying that[latex]\,x\,[/latex]is increasing without bound.
With the positive even-power function, as the input increases or decreases without bound, the output values become very large, positive numbers. Equivalently, we could describe this behavior by saying that as[latex]\,x\,[/latex]approaches positive or negative infinity, the[latex]\,f\left(x\right)\,[/latex]values increase without bound. In symbolic form, we could write
[latex]\text{as }x\to ±\infty , f\left(x\right)\to \infty[/latex]
Figure 13 shows the graphs of[latex]\,f\left(x\right)={x}^{3},\,g\left(x\right)={x}^{5},[/latex] and [latex]\,h\left(x\right)={x}^{7},[/latex] which are all power functions with odd, whole-number powers. Notice that these graphs look similar to the cubic function in the toolkit. Again, as the power increases, the graphs flatten near the origin and become steeper away from the origin.
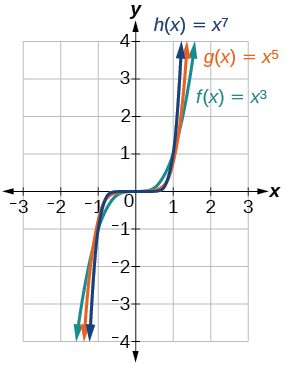
Figure 3 Odd-power functions
These examples illustrate that functions of the form[latex]\,f\left(x\right)={x}^{n}\,[/latex]reveal symmetry of one kind or another. First, in Figure 2, we see that even functions of the form[latex]\,f\left(x\right)={x}^{n}\text{, }n\,[/latex]even, are symmetric about the[latex]\,y\text{-}[/latex]axis. In Figure 3, we see that odd functions of the form[latex]\,f\left(x\right)={x}^{n}\text{, }n\,[/latex] odd, are symmetric about the origin.
For these odd power functions, as[latex]\,x\,[/latex] approaches negative infinity,[latex]\,f\left(x\right)\,[/latex] decreases without bound. As[latex]\,x\,[/latex] approaches positive infinity,[latex]\,f\left(x\right)\,[/latex] increases without bound. In symbolic form we write
[latex]\begin{array}{llllll}\text{as } x & \to & -\infty, & f\left(x\right) & \to &-\infty \\ \text{as } x & \to & \phantom{-}\infty, & f\left(x\right) & \to & \phantom{-}\infty \end{array}[/latex]
The behavior of the graph of a function as the input values get very small ([latex]\,x\to -\infty \,[/latex]) and get very large ([latex]\,x\to \infty \,[/latex]) is referred to as the end behavior of the function. We can use words or symbols to describe end behavior.
Figure 4 shows the end behavior of power functions in the form
[latex]f\left(x\right)=k{x}^{n}[/latex]
where[latex]\,n\,[/latex]is a non-negative integer depending on the power and the constant.
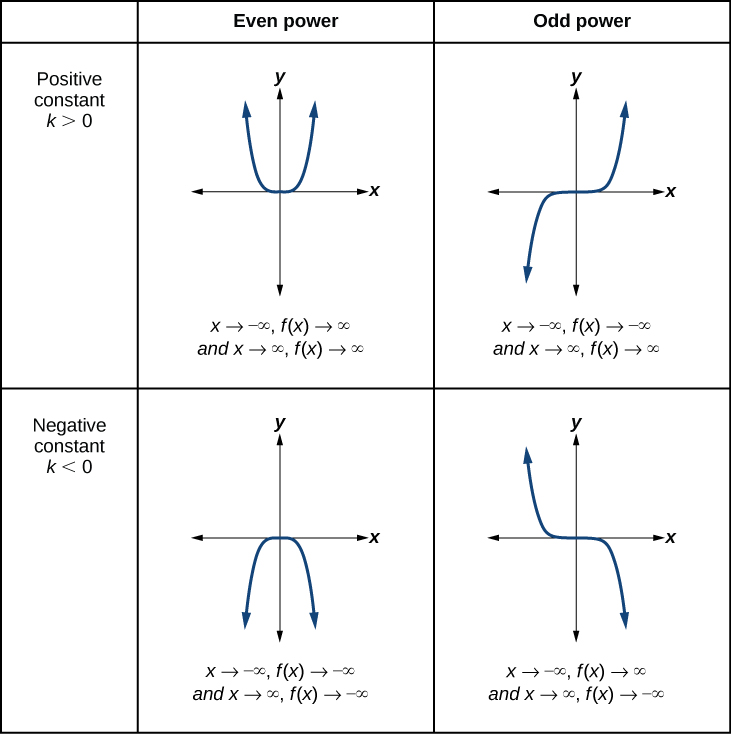
Figure 4
How To
Given a power function [latex]f\left(x\right)=k{x}^{p}[/latex], where n is a non-negative integer, identify the end behavior.
- Determine whether the power is even or odd.
- Determine whether the constant is positive or negative.
- Use Figure 4 to identify the end behavior.
EXAMPLE 2
Identifying the End Behavior of a Power Function
Describe the end behavior of the graph of[latex]\,f\left(x\right)={x}^{8}.[/latex]
Show/Hide Solution
 Solution
Solution
The coefficient is 1 (positive) and the exponent of the power function is 8 (an even number). As[latex]\,x\,[/latex]approaches infinity, the output (value of[latex]\,f\left(x\right)[/latex]) increases without bound. We write as
As[latex]\,x[/latex] approaches negative infinity, the output increases without bound. In symbolic form, as
We can graphically represent the function as shown in Figure 5.
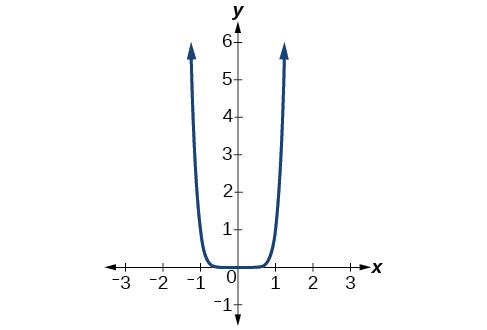
Figure 5
EXAMPLE 3
Identifying the End Behavior of a Power Function.
Describe the end behavior of the graph of[latex]\,f\left(x\right)={x}^{9}.[/latex]
Show/Hide Solution
 Solution
Solution
The exponent of the power function is 9 (an odd number). Because the coefficient is - 1 (negative), the graph is the reflection about the[latex]\,x[/latex]-axis of the graph of[latex]\,f\left(x\right)={x}^{9}.[/latex]
Figure 6 shows that as[latex]\,x\,[/latex]approaches infinity, the output decreases without bound. As[latex]\,x[/latex] approaches negative infinity, the output increases without bound. In symbolic form, we would write
[latex]\begin{array}{l}\text{as} x\to -\infty , f\left(x\right)\to \infty \\ \text{as} x\to \infty , f\left(x\right)\to -\infty \end{array}[/latex]
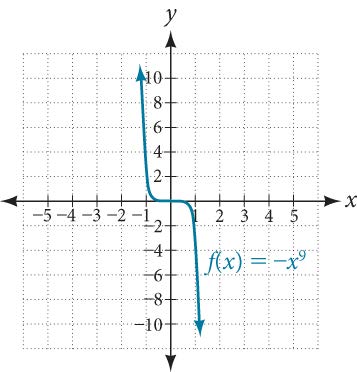
Figure 6
 Analysis
Analysis
We can check our work by using the table feature on a graphing utility.
| [latex]x[/latex] |
[latex]f\left(x\right)[/latex] |
| –10 |
1,000,000,000 |
| –5 |
1,953,125 |
| 0 |
0 |
| 5 |
–1,953,125 |
| 10 |
–1,000,000,000 |
Table 2
We can see from Table 2 that, when we substitute very small values for[latex]\,x[/latex], the output is very large, and when we substitute very large values for[latex]\,x,\,[/latex]the output is very small (meaning that it is a very large negative value).
 Try It #2
Try It #2
Describe in words and symbols the end behavior of[latex]\,f\left(x\right)=-5{x}^{4}.[/latex]
Identifying Polynomial Functions
An oil pipeline bursts in the Gulf of Mexico, causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius[latex]\,r\,[/latex] of the spill depends on the number of weeks[latex]\,w\,[/latex] that have passed. This relationship is linear.
[latex]r\left(w\right)=24+8w[/latex]
We can combine this with the formula for the area[latex]\,A\,[/latex] of a circle.
[latex]A\left(r\right)=\pi {r}^{2}[/latex]
Composing these functions gives a formula for the area in terms of weeks.
[latex]\begin{array}{ccc}\hfill A\left(w\right)& =& A\left(r\left(w\right)\right)\hfill \\ & =& A\left(24+8w\right)\hfill \\ & =& \pi {\left(24+8w\right)}^{2}\hfill \end{array}[/latex]
Multiplying gives the formula.
[latex]A\left(w\right)=576\pi +384\pi w+64\pi {w}^{2}[/latex]
This formula is an example of a polynomial function. A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
Polynomial Functions
Let[latex]\,n\,[/latex] be a non-negative integer. A polynomial function is a function that can be written in the form
[latex]f\left(x\right)={a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]
This is called the general form of a polynomial function.
Each[latex]\,{a}_{i}\,[/latex] is a coefficient and can be any real number, but[latex]\,{a}_{n}\,[/latex]cannot = 0.
Each expression[latex]\,{a}_{i}{x}^{i}\,[/latex] is a term of a polynomial function.
EXAMPLE 4
Identifying Polynomial Functions
Which of the following are polynomial functions?
Show/Hide Solution
 Solution
Solution
The first two functions are examples of polynomial functions because they can be written in the form
where the powers are non-negative integers and the coefficients are real numbers.
- [latex]f\left(x\right)\,[/latex]can be written as[latex]\,f\left(x\right)=6{x}^{4}+4.[/latex]
- [latex]g\left(x\right)\,[/latex]can be written as[latex]\,g\left(x\right)=-{x}^{3}+4x.[/latex]
- [latex]h\left(x\right)\,[/latex]cannot be written in this form and is therefore not a polynomial function.
Identifying the Degree and Leading Coefficient of a Polynomial Function
Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order of power, or in general form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the highest power of the variable, or the term with the highest degree. The leading coefficient is the coefficient of the leading term.
Terminology of Polynomial Functions
We often rearrange polynomials so that the powers are descending.
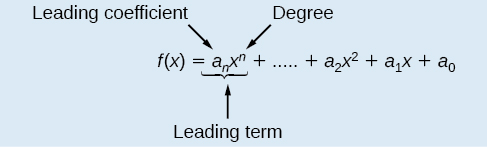
When a polynomial is written in this way, we say that it is in general form.
How To
Given a polynomial function, identify the degree and leading coefficient.
- Find the highest power of[latex]\,x,\,[/latex]to determine the degree of the function.
- Identify the term containing the highest power of[latex]\,x,\,[/latex]to find the leading term.
- Identify the coefficient of the leading term.
EXAMPLE 5
Identifying the Degree and Leading Coefficient of a Polynomial Function
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
[latex]\begin{array}{ccc}\hfill f\left(x\right)& =& 3+2{x}^{2}-4{x}^{3}\hfill \\ \hfill g\left(t\right)& =& 5{t}^{5}-2{t}^{3}+7t\hfill \\ h\left(p\right)\hfill & =& 6p-{p}^{3}-2\hfill \end{array}[/latex]
Show/Hide Solution
 Solution
Solution
For the function[latex]\,f\left(x\right),\,[/latex]the highest power of[latex]\,x\,[/latex]is [latex]\,3\,[/latex]so the degree is[latex]\,3.\,[/latex] The leading term is the term containing that degree,[latex]\,-4{x}^{3}.\,[/latex]The leading coefficient is the coefficient of that term,[latex]\,-4.[/latex]
For the function[latex]\,g\left(t\right),\,[/latex]the highest power of[latex]\,t\,[/latex]is[latex]\,5,\,[/latex]so the degree is[latex]\,5.\,[/latex]The leading term is the term containing that degree,[latex]\,5{t}^{5}.\,[/latex]The leading coefficient is the coefficient of that term,[latex]\,5.[/latex]
For the function[latex]\,h\left(p\right),\,[/latex]the highest power of[latex]\,p\,[/latex]is[latex]\,3,\,[/latex]so the degree is[latex]\,3.\,[/latex]The leading term is the term containing that degree,[latex]\,-{p}^{3}.\,[/latex]The leading coefficient is the coefficient of that term,[latex]\,-1.[/latex]
 Try It #3
Try It #3
Identify the degree, leading term, and leading coefficient of the polynomial
[latex]\,f\left(x\right)=4{x}^{2}-{x}^{6}+2x-6.[/latex]
Identifying End Behavior of Polynomial Functions
Knowing the degree of a polynomial function is useful in helping us predict its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the power function consisting of the leading term. See Table 3.
EXAMPLE 6
Identifying End Behavior and Degree of a Polynomial Function
Describe the end behavior and determine a possible degree of the polynomial function in Figure 7.
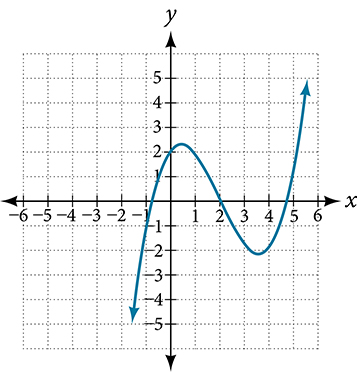
Figure 7
Show/Hide Solution
 Solution
Solution
As the input values[latex]\,x\,[/latex]get very large, the output values[latex]\,f\left(x\right)\,[/latex]increase without bound.
As the input values[latex]\,x\,[/latex]get very small, the output values[latex]\,f\left(x\right)\,[/latex]decrease without bound.
We can describe the end behavior symbolically by writing
[latex]\begin{array}{l}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to \infty \end{array}[/latex]
In words, we could say that as[latex]\,x\,[/latex]values approach infinity, the function values approach infinity, and as[latex]\,x\,[/latex]values approach negative infinity, the function values approach negative infinity.
We can tell this graph has the shape of an odd degree power function that has not been reflected, so the degree of the polynomial creating this graph must be odd and the leading coefficient must be positive.
 Try It #4
Try It #4
Describe the end behavior, and determine a possible degree of the polynomial function in Figure 8.
Figure 8
EXAMPLE 7
Identifying End Behavior and Degree of a Polynomial Function
Given the function[latex]\,f\left(x\right)=-3{x}^{2}\left(x-1\right)\left(x+4\right),\,[/latex]express the function as a polynomial in general form, and determine the leading term, degree, and end behavior of the function.
Show/Hide Solution
 Solution
Solution
Obtain the general form by expanding the given expression for[latex]\,f\left(x\right).[/latex]
[latex]\begin{array}{ccc}\hfill f\left(x\right)& =& -3{x}^{2}\left(x-1\right)\left(x+4\right)\hfill \\ & =& -3{x}^{2}\left({x}^{2}+3x-4\right)\hfill \\ & =& -3{x}^{4}-9{x}^{3}+12{x}^{2}\hfill \end{array}[/latex]
The general form is[latex]\,f\left(x\right)=-3{x}^{4}-9{x}^{3}+12{x}^{2}.\,[/latex]
The leading term is[latex]\,-3{x}^{4};\,[/latex] therefore, the degree of the polynomial is 4. The degree is even (4) and the leading coefficient is negative (–3), so the end behavior is
[latex]\begin{array}{l}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to -\infty \end{array}[/latex]
 Try It #5
Try It #5
Given the function[latex]\,f\left(x\right)=0.2\left(x-2\right)\left(x+1\right)\left(x-5\right),\,[/latex]express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
Identifying Local Behavior of Polynomial Functions
In addition to the end behavior of polynomial functions, we are also interested in what happens in the “middle” of the function. In particular, we are interested in locations where graph behavior changes. A turning point is a point at which the function values change from increasing to decreasing or decreasing to increasing.
We are also interested in the intercepts. As with all functions, the[latex]\,y[/latex]-intercept is the point at which the graph intersects the vertical axis. The point corresponds to the coordinate pair in which the input value is zero. Because a polynomial is a function, only one output value corresponds to each input value so there can be only one [latex]\,y[/latex]-intercept[latex]\,\left(0,{a}_{0}\right).\,[/latex]
The x-intercepts occur at the input values that correspond to an output value of zero. It is possible to have more than one [latex]\,x[/latex]-intercept. See Figure 9.
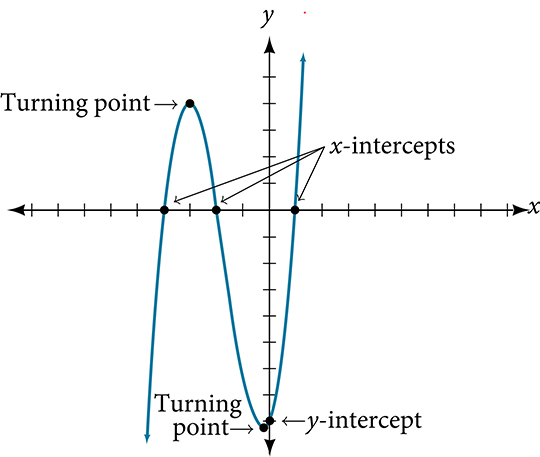
Figure 9
Intercepts and Turning Points of Polynomial Functions
A turning point of a graph is a point at which the graph changes direction from increasing to decreasing or decreasing to increasing.
The[latex]\,y-[/latex]intercept is the point at which the function has an input value of zero.
The[latex]\,x-[/latex]intercepts are the points at which the output value is zero.
How To
Given a polynomial function, determine the intercepts.
- Determine the[latex]\,y[/latex]-intercept by setting[latex]\,x[/latex]= 0 and finding the corresponding output value.
- Determine the[latex]\,x[/latex]-intercepts by solving for the input values that yield an output value of zero.
EXAMPLE 8
Determining the Intercepts of a Polynomial Function
Given the polynomial function
[latex]f\left(x\right)=\left(x-2\right)\left(x+1\right)\left(x-4\right)[/latex]
written in factored form for your convenience, determine the[latex]\,y[/latex]- and[latex]\,x[/latex]-intercepts.
Show/Hide Solution
 Solution
Solution
The[latex]\,y[/latex]-intercept occurs when the input is zero so substitute 0 for[latex]\,x.[/latex]
[latex]\begin{array}{ccc}\hfill f\left(0\right)& =& {\left(0\right)}^{4}-4{\left(0\right)}^{2}-45\hfill \\ & =& -45\hfill \end{array}[/latex]
The[latex]\,y[/latex]-intercept is[latex]\,\left(0,8\right).[/latex]
The[latex]\,x[/latex]-intercepts occur when the output is zero.
[latex]0=\left(x-2\right)\left(x+1\right)\left(x-4\right)[/latex]
[latex]\begin{array}{ccccccccccc}\hfill x-2& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x+1& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x-4& =& 0\hfill \\ \hfill x& =& 2\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x& =& -1\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x& =& 4\hfill \end{array}[/latex]
The[latex]\,x[/latex]-intercepts are[latex]\,\left(2,0\right),\left(–1,0\right),\,[/latex]and[latex]\,\left(4,0\right).[/latex]
We can see these intercepts on the graph of the function shown in Figure 10.
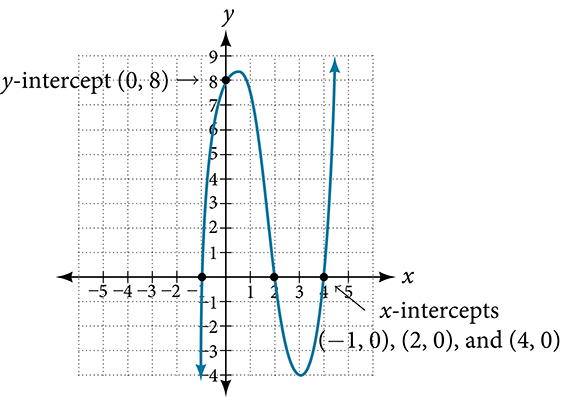
Figure 10
EXAMPLE 9
Determining the Intercepts of a Polynomial Function with Factoring
Given the polynomial function[latex]\,f\left(x\right)={x}^{4}-4{x}^{2}-45,\,[/latex]determine the the[latex]\,y[/latex]- and[latex]\,x[/latex]-intercepts.
Show/Hide Solution
 Solution
Solution
The[latex]\,y[/latex]-intercept occurs when the input is zero.
[latex]\begin{array}{ccc}\hfill f\left(0\right)& =& {\left(0\right)}^{4}-4{\left(0\right)}^{2}-45\hfill \\ & =& -45\hfill \end{array}[/latex]
The[latex]\,y[/latex]-intercept is[latex]\,\left(0,-45\right).[/latex]
The[latex]\,x[/latex]-intercepts occur when the output is zero. To determine when the output is zero, we will need to factor the polynomial.
[latex]\begin{array}{ccc}\hfill f\left(x\right)& =& {x}^{4}-4{x}^{2}-45\hfill \\ & =& \left({x}^{2}-9\right)\left({x}^{2}+5\right)\hfill \\ & =& \left(x-3\right)\left(x+3\right)\left({x}^{2}+5\right)\hfill \end{array}[/latex]
[latex]\phantom{\rule{2em}{0ex}}0=\left(x-3\right)\left(x+3\right)\left({x}^{2}+5\right)[/latex]
[latex]\begin{array}{ccccccccc}\hfill x-3& =& 0\hfill & \text{or}& \hfill x+3& =& 0\hfill &\text{or}& {x}^{2}+5=0\\ \hfill x& =& 3\hfill & \text{or} & \hfill x& =& -3\hfill & \text{or}& (\text{no real solution)}\end{array}[/latex]
The[latex]\,x[/latex]-intercepts are[latex]\,\left(3,0\right)\,[/latex]and[latex]\,\left(–3,0\right).[/latex]
We can see these intercepts on the graph of the function shown in Figure 11. We can see that the function is even because[latex]\,f\left(x\right)=f\left(-x\right).[/latex]
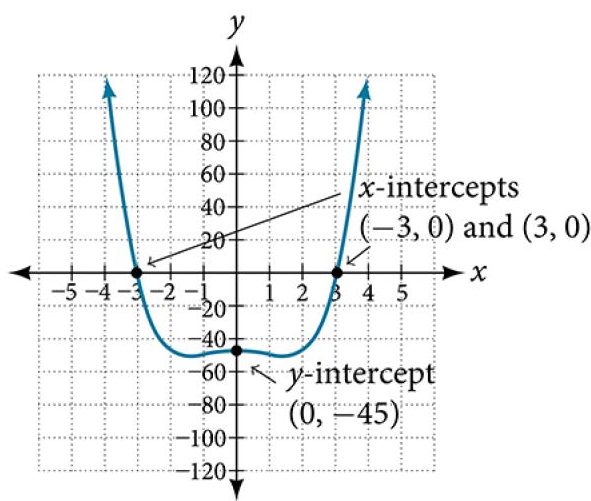
Figure 11
 Try It #6
Try It #6
Given the polynomial function[latex]\,f\left(x\right)=2{x}^{3}-6{x}^{2}-20x,\,[/latex]determine the[latex]\,y[/latex]- and[latex]\,x[/latex]-intercepts.
Comparing Smooth and Continuous Graphs
The degree of a polynomial function helps us to determine the number of the[latex]\,x[/latex]-intercepts and the number of turning points. A polynomial function of[latex]\,n\text{th}\,[/latex]degree is the product of[latex]\,n\,[/latex]factors, so it will have at most[latex]\,n\,[/latex]roots or zeros, or [latex]\,x[/latex]-intercepts.
The graph of the polynomial function of degree[latex]\,n\,[/latex]must have at most[latex]\,n–1\,[/latex]turning points. This means the graph has at most one fewer turning point than the degree of the polynomial or one fewer than the number of factors.
A continuous function has no breaks in its graph: the graph can be drawn without lifting the pen from the paper. A smooth curve is a graph that has no sharp corners. The turning points of a smooth graph must always occur at rounded curves. The graphs of polynomial functions are both continuous and smooth.
Intercepts and Turning Points of Polynomials
A polynomial of degree[latex]\,n\,[/latex]will have, at most,[latex]\,n\,[/latex][latex]\,x[/latex]-intercepts and[latex]\,n-1\,[/latex]turning points.
EXAMPLE 10
Determining the Number of Intercepts and Turning Points of a Polynomial
Without graphing the function, determine the local behavior of the function by finding the maximum number of[latex]\,x[/latex]-intercepts and turning points for[latex]\,f\left(x\right)=-3{x}^{10}+4{x}^{7}-{x}^{4}+2{x}^{3}.[/latex]
Show/Hide Solution
 Solution
Solution
The polynomial has a degree of 10, so there are at most 10[latex]\,x[/latex]-intercepts and at most 9 turning points.
 Try It #7
Try It #7
Without graphing the function, determine the maximum number of[latex]\,x[/latex]-intercepts and turning points for[latex]\,f\left(x\right)=108-13{x}^{9}-8{x}^{4}+14{x}^{12}+2{x}^{3}.[/latex]
EXAMPLE 11
Drawing Conclusions about a Polynomial Function from the Graph
What can we conclude about the polynomial represented by the graph shown in Figure 12 based on its intercepts and turning points?
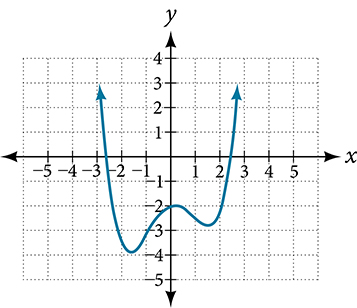
Figure 12
Show/Hide Solution
 Solution
Solution
The end behavior of the graph tells us this is the graph of an even-degree polynomial. See Figure 13.
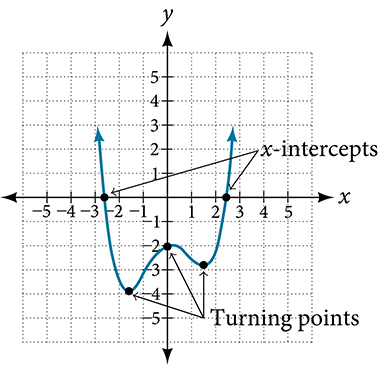
Figure 13
The graph has 2[latex]\,x[/latex]-intercepts, suggesting a degree of 2 or greater, and 3 turning points, suggesting a degree of 4 or greater. Based on this, it would be reasonable to conclude that the degree is even and at least 4.
 Try It #8
Try It #8
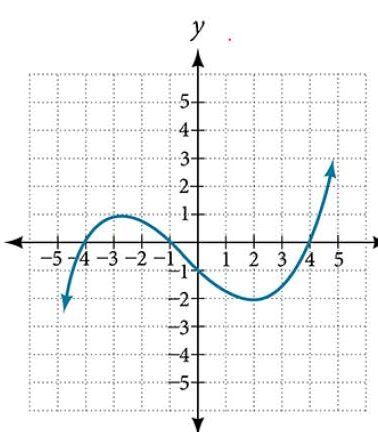
What can we conclude about the polynomial represented by the graph shown in Figure 14 based on its intercepts and turning points?
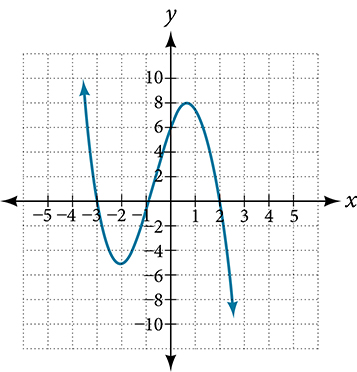
Figure 14
EXAMPLE 12
Drawing Conclusions about a Polynomial Function from the Factors
Given the function[latex]\,f\left(x\right)=-4x\left(x+3\right)\left(x-4\right),\,[/latex]determine the local behavior.
Show/Hide Solution
 Solution
Solution
The[latex]\,y[/latex]-intercept is found by evaluating[latex]\,f\left(0\right).[/latex]
[latex]\begin{array}{ccc}\hfill f\left(0\right)& =& -4\left(0\right)\left(0+3\right)\left(0-4\right)\\ & =& 0\hfill \end{array}[/latex]
The[latex]\,x[/latex]-intercept is[latex]\,\left(0,0\right).[/latex]
The[latex]\,x[/latex]-intercepts are found by determining the zeros of the function.
[latex]0=-4x\left(x+3\right)\left(x-4\right)[/latex]
[latex]\begin{array}{ccccccccccc}\hfill x& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x+3& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x-4& =& 0\hfill \\ x& =& 0& \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& x& =& -3& \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& x& =& 4\end{array}[/latex]
The[latex]\,x[/latex]-intercepts are[latex]\,\left(0,0\right),\left(–3,0\right),\,[/latex]and[latex]\,\left(4,0\right).[/latex]
The degree is 3 so the graph has at most 2 turning points.
 Try It #9
Try It #9
Given the function[latex]\,f\left(x\right)=0.2\left(x-2\right)\left(x+1\right)\left(x-5\right),\,[/latex]determine the local behavior.
Section 1.1 Part 1 Exercises
[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]
[Part 2 about Graphs of Polynomial Functions follows!]
Verbal
1. Explain the difference between the coefficient of a power function and its degree.
2. If a polynomial function is in factored form, what would be a good first step in order to determine the degree of the function?
3. In general, explain the end behavior of a power function with odd degree if the leading coefficient is positive.
4. What is the relationship between the degree of a polynomial function and the maximum number of turning points in its graph?
5. What can we conclude if, in general, the graph of a polynomial function exhibits the following end behavior? As [latex]x\to -\infty,\; f\left(x\right)\to -\infty[/latex] and as [latex]x\to \infty ,\; f\left(x\right)\to -\infty .[/latex]
Algebraic
For the following exercises, identify the function as a power function, a polynomial function, or neither.
6. [latex]f\left(x\right)={x}^{5}[/latex]
7. [latex]f\left(x\right)={\left({x}^{2}\right)}^{3}[/latex]
8. [latex]f\left(x\right)=x-{x}^{4}[/latex]
9. [latex]f\left(x\right)=\frac{{x}^{2}}{{x}^{2}-1}[/latex]
10. [latex]f\left(x\right)=2x\left(x+2\right){\left(x-1\right)}^{2}[/latex]
11. [latex]f\left(x\right)={3}^{x+1}[/latex]
For the following exercises, find the degree and leading coefficient for the given polynomial.
12. [latex]-3x{}^{4}[/latex]
13. [latex]7-2{x}^{2}[/latex]
14. [latex]-2{x}^{2}-3{x}^{5}+x-6[/latex]
15. [latex]x\left(4-{x}^{2}\right)\left(2x+1\right)[/latex]
16. [latex]{x}^{2}{\left(2x-3\right)}^{2}[/latex]
For the following exercises, determine the end behavior of the functions.
17. [latex]f\left(x\right)={x}^{4}[/latex]
18. [latex]f\left(x\right)={x}^{3}[/latex]
19. [latex]f\left(x\right)=-{x}^{4}[/latex]
20. [latex]f\left(x\right)=-{x}^{9}[/latex]
21. [latex]f\left(x\right)=-2{x}^{4}-3{x}^{2}+x-1[/latex]
22. [latex]f\left(x\right)=3{x}^{2}+x-2[/latex]
23. [latex]f\left(x\right)={x}^{2}\left(2{x}^{3}-x+1\right)[/latex]
24. [latex]f\left(x\right)={\left(2-x\right)}^{7}[/latex]
For the following exercises, find the intercepts of the functions.
25. [latex]f\left(t\right)=2\left(t-1\right)\left(t+2\right)\left(t-3\right)[/latex]
26. [latex]g\left(n\right)=-2\left(3n-1\right)\left(2n+1\right)[/latex]
27. [latex]f\left(x\right)={x}^{4}-16[/latex]
28. [latex]f\left(x\right)={x}^{3}+27[/latex]
29. [latex]f\left(x\right)=x\left({x}^{2}-2x-8\right)[/latex]
30. [latex]f\left(x\right)=\left(x+3\right)\left(4{x}^{2}-1\right)[/latex]
Graphical
For the following exercises, determine the least possible degree of the polynomial function shown.
31. 
32. 
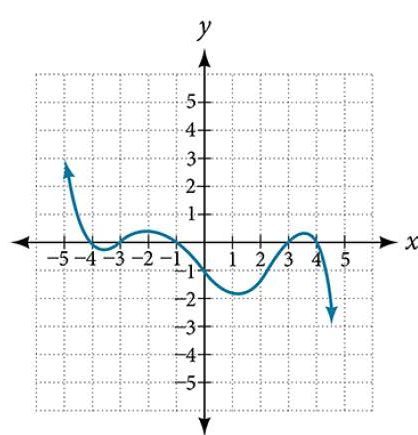
33. 
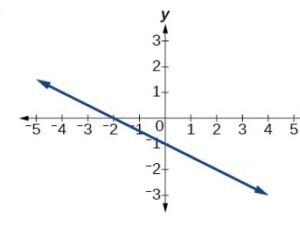
34. 
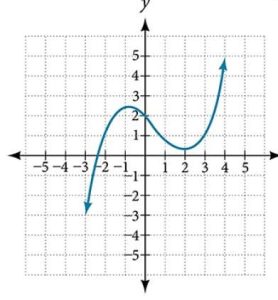
35. 
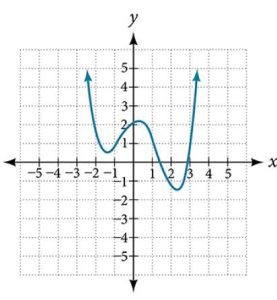
36. 
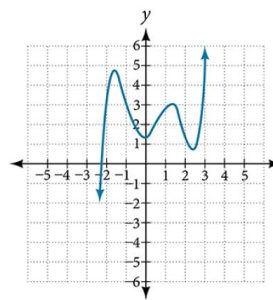
37. 
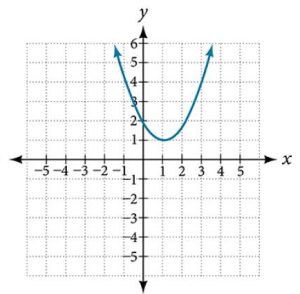
38. 
For the following exercises, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
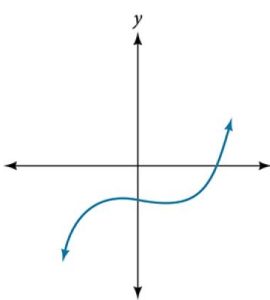
39. 
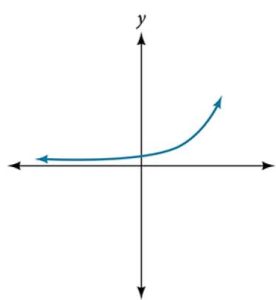
40. 
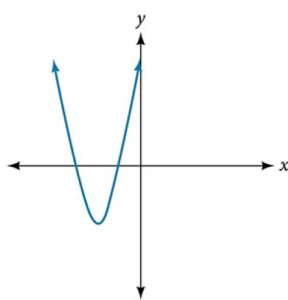
41. 
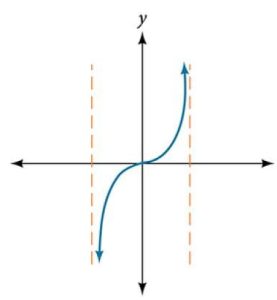
42. 
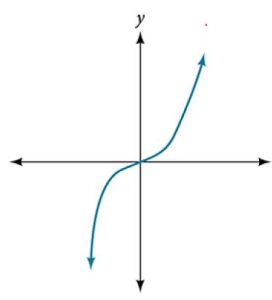
43. 
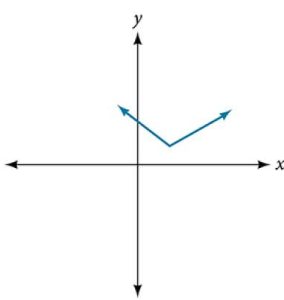
44. 
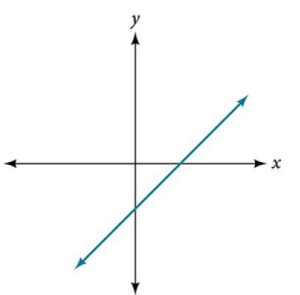
45. 
Numeric
For the following exercises, make a table to confirm the end behavior of the function.
46. [latex]f\left(x\right)=-{x}^{3}[/latex]
47. [latex]f\left(x\right)={x}^{4}-5{x}^{2}[/latex]
48. [latex]f\left(x\right)={x}^{2}{\left(1-x\right)}^{2}[/latex]
49. [latex]f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(3-x\right)[/latex]
50. [latex]f\left(x\right)=\frac{{x}^{5}}{10}-{x}^{4}[/latex]
Technology
For the following exercises, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.
51. [latex]f\left(x\right)={x}^{3}\left(x-2\right)[/latex]
52. [latex]f\left(x\right)=x\left(x-3\right)\left(x+3\right)[/latex]
53. [latex]f\left(x\right)=x\left(14-2x\right)\left(10-2x\right)[/latex]
54. [latex]f\left(x\right)=x\left(14-2x\right){\left(10-2x\right)}^{2}[/latex]
55. [latex]f\left(x\right)={x}^{3}-16x[/latex]
56. [latex]f\left(x\right)={x}^{3}-27[/latex]
57. [latex]f\left(x\right)={x}^{4}-81[/latex]
58. [latex]f\left(x\right)=-{x}^{3}+{x}^{2}+2x[/latex]
59. [latex]f\left(x\right)={x}^{3}-2{x}^{2}-15x[/latex]
60. [latex]f\left(x\right)={x}^{3}-0.01x[/latex]
Extensions
For the following exercises, use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is 1 or –1. There may be more than one correct answer.
61. The[latex]\,y-[/latex]intercept is[latex]\,\left(0,-4\right).\,[/latex]The[latex]\,x-[/latex]intercepts are[latex]\,\left(-2,0\right),\,\left(2,0\right).\,[/latex]Degree is 2.
End behavior:[latex]\,\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty .[/latex]
62. The[latex]\,y-[/latex]intercept is[latex]\,\left(0,9\right).\,[/latex]The[latex]\,x\text{-}[/latex]intercepts are[latex]\,\left(-3,0\right),\,\left(3,0\right).\,[/latex]Degree is 2.
End behavior:[latex]\,\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty .[/latex]
63. The[latex]\,y-[/latex]intercept is[latex]\,\left(0,0\right).\,[/latex]The[latex]\,x-[/latex]intercepts are[latex]\,\left(0,0\right),\,\left(2,0\right).\,[/latex]Degree is 3.
End behavior:[latex]\,\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty .[/latex]
64. The[latex]\,y-[/latex]intercept is[latex]\,\left(0,1\right).\,[/latex]The[latex]\,x-[/latex]intercept is[latex]\,\left(1,0\right).\,[/latex]Degree is 3.
End behavior:[latex]\,\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty .[/latex]
65. The[latex]\,y-[/latex]intercept is[latex]\,\left(0,1\right).\,[/latex]There is no[latex]\,x-[/latex]intercept. Degree is 4.
End behavior:[latex]\,\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty .[/latex]
Real-World Applications
For the following exercises, use the written statements to construct a polynomial function that represents the required information.
66. An oil slick is expanding as a circle. The radius of the circle is increasing at the rate of 20 meters per day. Express the area of the circle as a function of [latex]d[/latex], the number of days elapsed.
67. A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of [latex]m[/latex], the number of minutes elapsed.
68. A rectangle has a length of 10 inches and a width of 6 inches. If the length is increased by x inches and the width increased by twice that amount, express the area of the rectangle as a function of [latex]x[/latex].
69. An open box is to be constructed by cutting out square corners of [latex]x-[/latex]inch sides from a piece of cardboard 8 inches by 8 inches and then folding up the sides. Express the volume of the box as a function of [latex]x[/latex].
70. A rectangle is twice as long as it is wide. Squares of side 2 feet are cut out from each corner. Then the sides are folded up to make an open box. Express the volume of the box as a function of the width ([latex]x[/latex]).
Answers to Section 1.1 Part 1 Odd Problems
1. The coefficient of the power function is the real number that is multiplied by the variable raised to a power. The degree is the highest power appearing in the function.
3. As [latex]x[/latex] decreases without bound, so does [latex]f\left(x\right)[/latex]. As [latex]x[/latex] increases without bound, so does [latex]f\left(x\right)[/latex].
5. The polynomial function is of even degree and leading coefficient is negative.
7. Power function
9. Neither
11. Neither
13. Degree = 2, Coefficient = –2
15. Degree =4, Coefficient = –2
17. [latex]\text{As}\,x\to \infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to -\infty ,\,f\left(x\right)\to \infty[/latex]
19. [latex]\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty[/latex]
21. [latex]\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty[/latex]
23. [latex]\text{As}\,x\to \infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to -\infty ,\,f\left(x\right)\to -\infty[/latex]
25. [latex]y-[/latex]intercept is[latex]\,\left(0,12\right),\,[/latex][latex]t-[/latex]intercepts are[latex]\,\left(1,0\right);\left(–2,0\right);\text{and }\left(3,0\right).[/latex]
27. [latex]y-[/latex]intercept is[latex]\,\left(0,-16\right).\,[/latex][latex]x-[/latex]intercepts are[latex]\,\left(2,0\right)\,[/latex]and[latex]\,\left(-2,0\right).[/latex]
29. [latex]y-[/latex]intercept is[latex]\,\left(0,0\right).\,[/latex][latex]x-[/latex]intercepts are[latex]\,\left(0,0\right),\left(4,0\right),\,[/latex]and[latex]\,\left(-2, 0\right).[/latex]
31. 3
33. 5
35. 3
37. 5
39. Yes. Number of turning points is 2. Least possible degree is 3.
41. Yes. Number of turning points is 1. Least possible degree is 2.
43. Yes. Number of turning points is 0. Least possible degree is 1.
45. Yes. Number of turning points is 0. Least possible degree is 1.
47.
| [latex]x[/latex] |
[latex]f\left(x\right)[/latex] |
|
10
|
9,500
|
|
100
|
99,950,000
|
|
-10
|
9,500
|
|
-100
|
99,950,000
|
As [latex]x \to -\infty, \; f\left(x\right) \to \infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to \infty[/latex]
49.
| [latex]x[/latex] |
[latex]f\left(x\right)[/latex] |
|
10
|
-504
|
|
100
|
-941,094
|
|
-10
|
1,716
|
|
-100
|
1,061,106
|
As [latex]x \to -\infty, \; f\left(x\right) \to \infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to -\infty[/latex]
51. 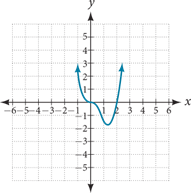
[latex]y-[/latex]intercept is (0,0), [latex]x-[/latex]intercepts are (0,0) and (2,0)
As [latex]x \to -\infty, \; f\left(x\right) \to \infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to \infty[/latex]
53. 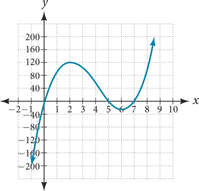
[latex]y-[/latex]intercept is (0,0), [latex]x-[/latex]intercepts are (0,0); (5,0); and (7,0)
As [latex]x \to -\infty, \; f\left(x\right) \to -\infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to \infty[/latex]
55. 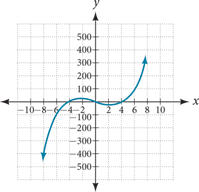
[latex]y-[/latex]intercept is (0,0), [latex]x-[/latex]intercepts are (-4,0); (0,0); and (4,0)
As [latex]x \to -\infty, \; f\left(x\right) \to -\infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to \infty[/latex]
57. 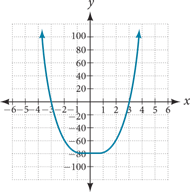
[latex]y-[/latex]intercept is (0,-81), [latex]x-[/latex]intercepts are (-3,0) and (3,0)
As [latex]x \to -\infty, \; f\left(x\right) \to \infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to \infty[/latex]
59. 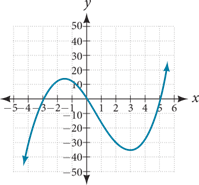
[latex]y-[/latex]intercept is (0,0), [latex]x-[/latex]intercepts are (-3,0); (0,0) and (5,0)
As [latex]x \to -\infty, \; f\left(x\right) \to -\infty \;\;\text{and as} \;\; x \to \infty, \; f\left(x\right) \to \infty[/latex]
61. [latex]f\left(x\right)={x}^{2}-4[/latex]
63. [latex]f\left(x\right)={x}^{3}-4{x}^{2}+4x[/latex]
65. [latex]f\left(x\right)={x}^{4}+1[/latex]
67. [latex]V\left(m\right)=8{m}^{3}+36{m}^{2}+54m+27[/latex]
69. [latex]V\left(x\right)=4{x}^{3}-32{x}^{2}+64x[/latex]
Section 1.1 Part 2: Graphs of Polynomial Functions
This content comes directly from OpenStax's textbook Algebra and Trigonometry Section 5.3 Graphs of Polynomial Functions.
Learning Objectives
In this section, you will:
- Recognize characteristics of graphs of polynomial functions. Use factoring to find zeros of polynomial functions.
- Identify zeros and their multiplicities. Determine end behavior.
- Understand the relationship between degree and turning points. Graph polynomial functions.
- Use the Intermediate Value Theorem.
Let's Get Started...
The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in Table 1.
| Year |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
| Revenues |
52.4 |
52.8 |
51.2 |
49.5 |
48.6 |
48.6 |
48.7 |
47.1 |
Table 1
The revenue can be modeled by the polynomial function
[latex]R\left(t\right)=-0.037{t}^{4}+1.414{t}^{3}-19.777{t}^{2}+118.696t-205.332[/latex]
where[latex]\,R\,[/latex]represents the revenue in millions of dollars and[latex]\,t\,[/latex]represents the year, with[latex]\,t=6\,[/latex]corresponding to 2006. Over which intervals is the revenue for the company increasing? Over which intervals is the revenue for the company decreasing? These questions, along with many others, can be answered by examining the graph of the polynomial function. We have already explored the local behavior of quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.
Recognizing Characteristics of Graphs of Polynomial Functions
Polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. Figure 1 shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.
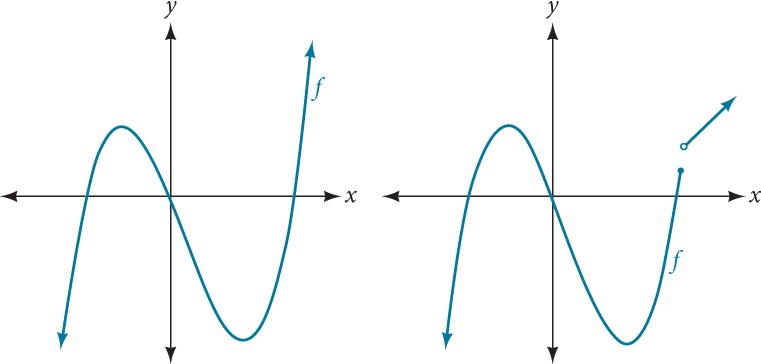
Figure 1
EXAMPLE 1
Recognizing Polynomial Functions
Which of the graphs in Figure 2 represents a polynomial function?
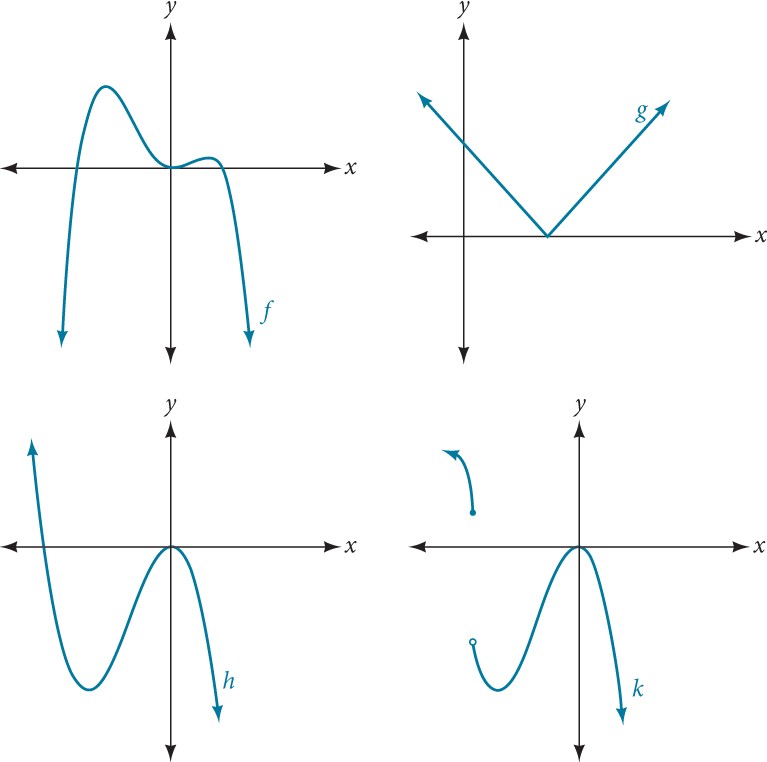
Figure 2
Show/Hide Solution
 Solution
Solution
The graphs of[latex]\,f\,[/latex]and[latex]\,h\,[/latex]are graphs of polynomial functions. They are smooth and continuous.
The graphs of[latex]\,g\,[/latex]and[latex]\,k\,[/latex]are graphs of functions that are not polynomials. The graph of function[latex]\,g\,[/latex]has a sharp corner. The graph of function[latex]\,k\,[/latex]is not continuous.
 Q&A
Q&A
Do all polynomial functions have as their domain all real numbers?
Yes. Any real number is a valid input for a polynomial function.
Using Factoring to Find Zeros of Polynomial Functions
Recall that if[latex]\,f\,[/latex]is a polynomial function, the values of[latex]\,x\,[/latex]for which[latex]\,f\left(x\right)=0\,[/latex]are called zeros of[latex]\,f.\,[/latex]If the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros.
We can use this method to find[latex]\,x\text{-}[/latex]intercepts because at the[latex]\,x\text{-}[/latex]intercepts we find the input values when the output value is zero. For general polynomials, this can be a challenging prospect. While quadratics can be solved using the relatively simple quadratic formula, the corresponding formulas for cubic and fourth-degree polynomials are not simple enough to remember, and formulas do not exist for general higher-degree polynomials. Consequently, we will limit ourselves to three cases:
- The polynomial can be factored using known methods: greatest common factor and trinomial factoring.
- The polynomial is given in factored form.
- Technology is used to determine the intercepts.
How To:
Given a polynomial function[latex]\,f,\,[/latex]find the[latex]\,x\text{-}[/latex]intercepts by factoring.
- Set[latex]\,f\left(x\right)=0.\,[/latex]
- If the polynomial function is not given in factored form:
- Factor out any common monomial factors.
- Factor any factorable binomials or trinomials.
- Set each factor equal to zero and solve to find the[latex]\,x\text{-}[/latex]intercepts.
EXAMPLE 2
Finding the [latex]\,x\text{-}[/latex]intercepts of a Polynomial Function by Factoring
Find the[latex]\,x\text{-}[/latex]intercepts of[latex]\,f\left(x\right)={x}^{6}-3{x}^{4}+2{x}^{2}.[/latex]
Show/Hide Solution
 Solution
Solution
We can attempt to factor this polynomial to find solutions for [latex]\,f\left(x\right)=0.[/latex]
[latex]\begin{array}{cccc}\hfill {x}^{6}-3{x}^{4}+2{x}^{2}& =& 0\hfill & \phantom{\rule{2em}{0ex}}\begin{array}{c}\text{Factor out the greatest}\hfill \\ \text{common factor}\text{.}\hfill \end{array}\hfill \\ \hfill {x}^{2}\left({x}^{4}-3{x}^{2}+2\right)& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{Factor the trinomial}\text{.}\hfill \\ \hfill {x}^{2}\left({x}^{2}-1\right)\left({x}^{2}-2\right)& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{Set each factor equal to zero}\text{.}\end{array}[/latex]
[latex]\begin{array}{ccccccccccc}& & & & \hfill \left({x}^{2}-1\right)& =& 0\hfill & & \hfill \left({x}^{2}-2\right)& =& 0\hfill \\ \hfill {x}^{2}& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}& \hfill {x}^{2}& =& 1\hfill & \phantom{\rule{2em}{0ex}}\text{or}& \hfill {x}^{2}& =& 2\hfill \\ \hfill x& =& 0\hfill & & \hfill x& =& ±1\hfill & & \hfill x& =& ±\sqrt{2}\hfill \end{array}[/latex]
This gives us five[latex]\,x\text{-}[/latex]intercepts:[latex]\,\left(0,0\right),\left(1,0\right),\left(-1,0\right),\left(\sqrt{2},0\right),\,[/latex]and[latex]\,\left(-\sqrt{2},0\right).\,[/latex]See Figure 3.
We can see that this is an even function because it is symmetric about the[latex]\,y\text{-}[/latex]axis.
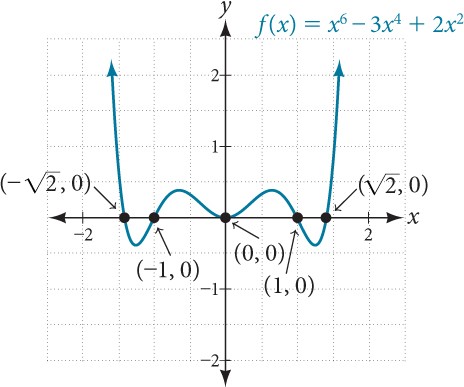
Figure 3
EXAMPLE 3
Finding the[latex]\,x\text{-}[/latex]intercepts of a Polynomial Function by Factoring
Find the[latex]\,x\text{-}[/latex]intercepts of[latex]\,f\left(x\right)={x}^{3}-5{x}^{2}-x+5.[/latex]
Show/Hide Solution
 Solution
Solution
Find solutions for[latex]\,f\left(x\right)=0\,[/latex]by factoring.
[latex]\begin{array}{cccc}\hfill {x}^{3}-5{x}^{2}-x+5& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{Factor by grouping}\text{.}\hfill \\ \hfill {x}^{2}\left(x-5\right)-\left(x-5\right)& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{Factor out the common factor}\text{.}\hfill \\ \hfill \left({x}^{2}-1\right)\left(x-5\right)& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{Factor the difference of squares}\text{.}\hfill \\ \hfill \left(x+1\right)\left(x-1\right)\left(x-5\right)& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{Set each factor equal to zero}\text{.}\hfill \end{array}[/latex]
[latex]\begin{array}{ccccccccccc}\hfill x+1& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x-1& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x-5& =& 0\hfill \\ \hfill x& =& -1\hfill & & \hfill x& =& 1\hfill & & \hfill x& =& 5\hfill \end{array}[/latex]
There are three[latex]\,x\text{-}[/latex]intercepts:[latex]\,\left(-1,0\right),\left(1,0\right),\,[/latex]and[latex]\,\left(5,0\right).\,[/latex]See Figure 4.
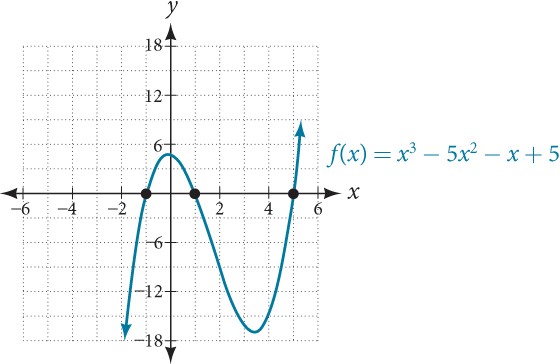
Figure 4
EXAMPLE 4
Finding the[latex]\,y\text{-}[/latex] and[latex]\,x\text{-}[/latex]intercepts of a Polynomial in Factored Form
Find the[latex]\,y\text{-}[/latex] and[latex]\,x\text{-}[/latex]intercepts of[latex]\,g\left(x\right)={\left(x-2\right)}^{2}\left(2x+3\right).[/latex]
Show/Hide Solution
 Solution
Solution
The[latex]\,y\text{-}[/latex]intercept can be found by evaluating[latex]\,g\left(0\right).[/latex]
[latex]\begin{array}{ccc}\hfill g\left(0\right)& =& {\left(0-2\right)}^{2}\left(2\left(0\right)+3\right)\hfill \\ & =& 12\hfill \end{array}[/latex]
So the[latex]\,y\text{-}[/latex]intercept is[latex]\,\left(0,12\right).[/latex]
The[latex]\,x\text{-}[/latex]intercepts can be found by solving[latex]\,g\left(x\right)=0.[/latex]
[latex]{\left(x-2\right)}^{2}\left(2x+3\right)=0[/latex]
[latex]\begin{array}{ccccccc}\hfill {\left(x-2\right)}^{2}& =& 0\hfill & & \hfill \left(2x+3\right)& =& 0\hfill \\ \hfill x-2& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x& =& -\frac{3}{2}\hfill \\ \hfill x& =& 2\hfill & & & & \end{array}[/latex]
So the[latex]\,x\text{-}[/latex]intercepts are[latex]\,\left(2,0\right)\,[/latex]and[latex]\,\left(-\frac{3}{2},0\right).[/latex]
 Analysis
Analysis
We can always check that our answers are reasonable by using a graphing calculator to graph the polynomial as shown in Figure 5.
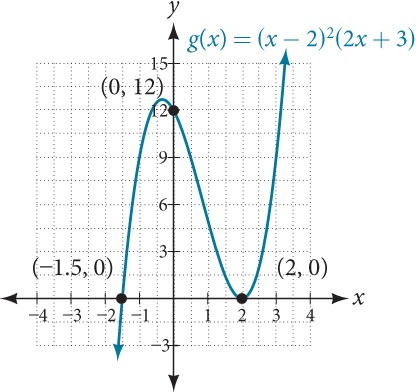
Figure 5
EXAMPLE 5
Finding the[latex]\,x\text{-}[/latex]intercepts of a Polynomial Function Using a Graph
Find the[latex]\,x\text{-}[/latex]intercepts of[latex]\,h\left(x\right)={x}^{3}+4{x}^{2}+x-6.[/latex]
Show/Hide Solution
 Solution
Solution
This polynomial is not in factored form, has no common factors, and does not appear to be factorable using techniques previously discussed. Fortunately, we can use technology to find the intercepts. Keep in mind that some values make graphing difficult by hand. In these cases, we can take advantage of graphing utilities.
Looking at the graph of this function, as shown in Figure 6, it appears that there are[latex]\,x\text{-}[/latex]intercepts at[latex]\,x=-3,-2,\,[/latex]and[latex]\,1.[/latex]
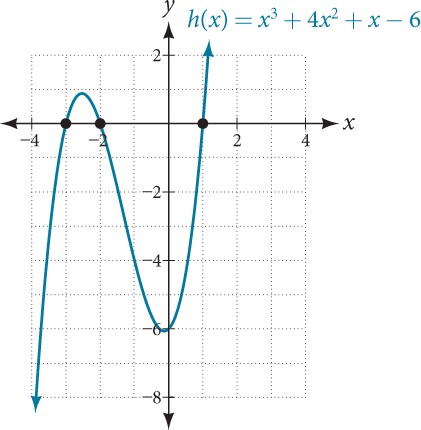
Figure 6
We can check whether these are correct by substituting these values for[latex]\,x\,[/latex]and verifying that
[latex]h\left(-3\right)=h\left(-2\right)=h\left(1\right)=0[/latex]
Since[latex]\,h\left(x\right)={x}^{3}+4{x}^{2}+x-6,\,[/latex]we have:
[latex]\begin{array}{ccc}\hfill h\left(-3\right)& =& {\left(-3\right)}^{3}+4{\left(-3\right)}^{2}+\left(-3\right)-6=-27+36-3-6=0\hfill \\ \hfill h\left(-2\right)& =& {\left(-2\right)}^{3}+4{\left(-2\right)}^{2}+\left(-2\right)-6=-8+16-2-6=0\hfill \\ \hfill h\left(1\right)& =& {\left(1\right)}^{3}+4{\left(1\right)}^{2}+\left(1\right)-6=1+4+1-6=0\hfill \end{array}[/latex]
Each[latex]\,x\text{-}[/latex]intercept corresponds to a zero of the polynomial function and each zero yields a factor, so we can now write the polynomial in factored form.
[latex]\begin{array}{ccc}\hfill h\left(x\right)& =& {x}^{3}+4{x}^{2}+x-6\hfill \\ & =& \left(x+3\right)\left(x+2\right)\left(x-1\right)\hfill \end{array}[/latex]
 Try It #1
Try It #1
Find the[latex]\,y\text{-}[/latex] and[latex]\,x\text{-}[/latex]intercepts of the function[latex]\,f\left(x\right)={x}^{4}-19{x}^{2}+30x.[/latex]
Identifying Zeros and Their Multiplicities
Graphs behave differently at various[latex]\,x\text{-}[/latex]intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and "bounce" off.
Suppose, for example, we graph the function shown.
[latex]f\left(x\right)=\left(x+3\right){\left(x-2\right)}^{2}{\left(x+1\right)}^{3}[/latex]
Notice in Figure 7 that the behavior of the function at each of the[latex]\,x\text{-}[/latex]intercepts is different.
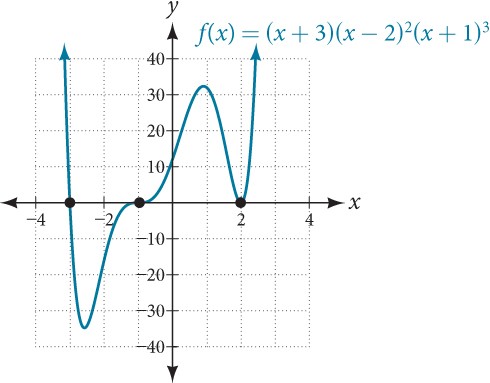
Figure 7 Identifying the behavior of the graph at an[latex]\,x\text{-}[/latex]intercept by examining the multiplicity of the zero.
The[latex]\,x\text{-}[/latex]intercept[latex]\,x=-3\,[/latex]is the solution of equation[latex]\,\left(x+3\right)=0.\,[/latex]The graph passes directly through the x-intercept at[latex]\,x=-3.\,[/latex]The factor is linear (has a degree of 1), so the behavior near the intercept is like that of a line—it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.
The[latex]\,x\text{-}[/latex]intercept[latex]\,x=2\,[/latex]is the repeated solution of equation[latex]\,{\left(x-2\right)}^{2}=0.\,[/latex]The graph touches the axis at the intercept and changes direction. The factor is quadratic (degree 2), so the behavior near the intercept is like that of a quadratic—it bounces off of the horizontal axis at the intercept.
[latex]{\left(x-2\right)}^{2}=\left(x-2\right)\left(x-2\right)[/latex]
The factor is repeated, that is, the factor[latex]\,\left(x-2\right)\,[/latex]appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. The zero associated with this factor,[latex]\,x=2,\,[/latex]has multiplicity 2 because the factor[latex]\,\left(x-2\right)\,[/latex]occurs twice.
The[latex]\,x\text{-}[/latex]intercept[latex]\,x=-1\,[/latex]is the repeated solution of factor[latex]\,{\left(x+1\right)}^{3}=0.\,[/latex]The graph passes through the axis at the intercept, but flattens out a bit first. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic—with the same S-shape near the intercept as the toolkit function[latex]\,f\left(x\right)={x}^{3}.\,[/latex]We call this a triple zero, or a zero with multiplicity 3.
For zeros with even multiplicities, the graphs touch or are tangent to the x-axis. For zeros with odd multiplicities, the graphs cross or intersect the x-axis. See Figure 8 for examples of graphs of polynomial functions with multiplicity 1, 2, and 3.
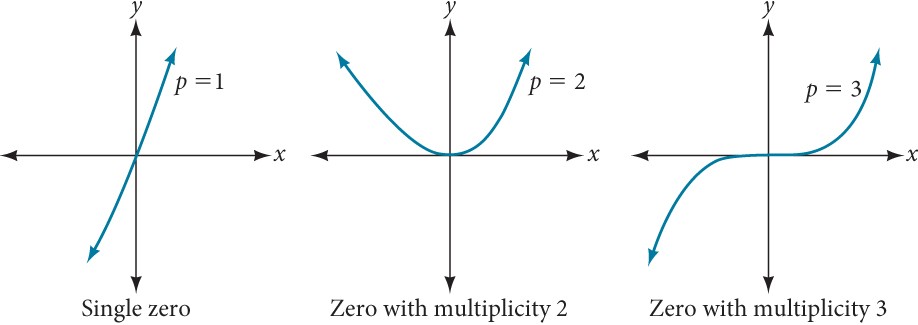
Figure 8
For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the[latex]\,x\text{-}[/latex]axis.
For higher odd powers, such as 5, 7, and 9, the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the[latex]\,x\text{-}[/latex]axis.
Graphical Behavior of Polynomials at[latex]\,x\text{-}[/latex]Intercepts
If a polynomial contains a factor of the form[latex]\,{\left(x-h\right)}^{p},\,[/latex]the behavior near the[latex]\,x\text{-}[/latex]intercept[latex]\,h\,[/latex]is determined by the power[latex]\,p.\,[/latex]We say that[latex]\,x=h\,[/latex]is a zero of multiplicity[latex]\,p.[/latex]
- The graph of a polynomial function will touch the[latex]\,x\text{-}[/latex]axis at zeros with even multiplicities.
- The graph will cross the[latex]\,x\text{-}[/latex]axis at zeros with odd multiplicities.
- The sum of the multiplicities is the degree of the polynomial function.
How To
Given a graph of a polynomial function of degree[latex]\,n[/latex], identify the zeros and their multiplicities.
- If the graph crosses the[latex]\,x\text{-}[/latex]axis and appears almost linear at the intercept, it is a single zero.
- If the graph touches the[latex]\,x\text{-}[/latex]axis and bounces off of the axis, it is a zero with even multiplicity.
- If the graph crosses the[latex]\,x\text{-}[/latex]axis at a zero, it is a zero with odd multiplicity.
- The sum of the multiplicities is[latex]\,n[/latex].
EXAMPLE 6
Identifying Zeros and Their Multiplicities
Use the graph of the function of degree 6 in Figure 9 to identify the zeros of the function and their possible multiplicities.
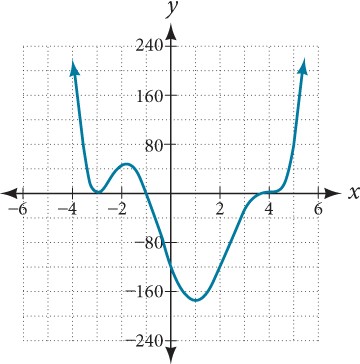
Figure 9
Show/Hide Solution
 Solution
Solution
The polynomial function is of degree 6. The sum of the multiplicities must be 6.
Starting from the left, the first zero occurs at[latex]\,x=-3.\,[/latex]The graph touches the[latex]\,x\text{-}[/latex]axis, so the multiplicity of the zero must be even. The zero of[latex]\,-3\,[/latex]most likely has multiplicity[latex]\,2.[/latex]
The next zero occurs at[latex]\,x=-1.\,[/latex]The graph looks almost linear at this point. This is a single zero of multiplicity 1.
The last zero occurs at[latex]\,x=4.\,[/latex]The graph crosses the[latex]\,x\text{-}[/latex]axis, so the multiplicity of the zero must be odd. We know that the multiplicity is likely 3 and that the sum of the multiplicities is 6.
 Try It #2
Try It #2
Use the graph of the function of degree 9 in Figure 10 to identify the zeros of the function and their multiplicities.
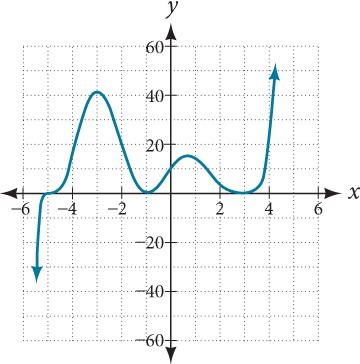
Figure 10
Determining End Behavior
As we have already learned, the behavior of a graph of a polynomial function of the form
[latex]f\left(x\right)={a}_{n}{x}^{n}+{a}_{n-1}{x}^{n-1}+...+{a}_{1}x+{a}_{0}[/latex]
will either ultimately rise or fall as[latex]\,x\,[/latex]increases without bound and will either rise or fall as[latex]\,x\,[/latex]decreases without bound. This is because for very large inputs, say 100 or 1,000, the leading term dominates the size of the output. The same is true for very small inputs, say –100 or –1,000.
Recall that we call this behavior the end behavior of a function. As we pointed out when discussing quadratic equations, when the leading term of a polynomial function,[latex]\,{a}_{n}{x}^{n},\,[/latex]is an even power function, as[latex]\,x\,[/latex]increases or decreases without bound,[latex]\,f\left(x\right)\,[/latex]increases without bound. When the leading term is an odd power function, as[latex]\,x\,[/latex]decreases without bound,[latex]\,f\left(x\right)\,[/latex]also decreases without bound; as[latex]\,x\,[/latex]increases without bound,[latex]\,f\left(x\right)\,[/latex]also increases without bound. If the leading term is negative, it will change the direction of the end behavior.
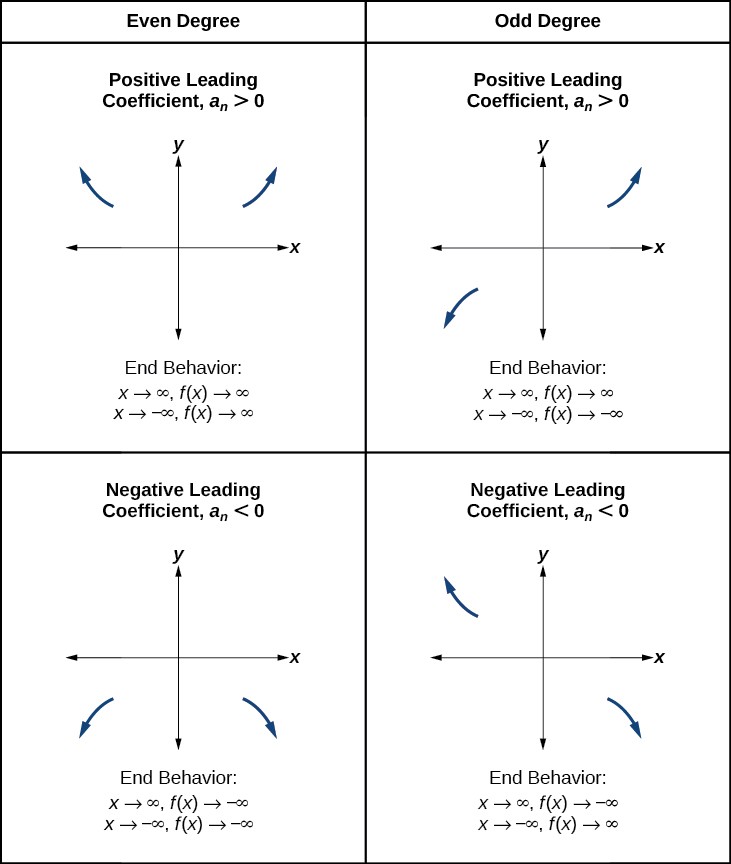
Figure 11
Understanding the Relationship between Degree and Turning Points
In addition to the end behavior, recall that we can analyze a polynomial function’s local behavior. It may have a turning point where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). Look at the graph of the polynomial function[latex]\,f\left(x\right)={x}^{4}-{x}^{3}-4{x}^{2}+4x\,[/latex]in Figure 12. The graph has three turning points.
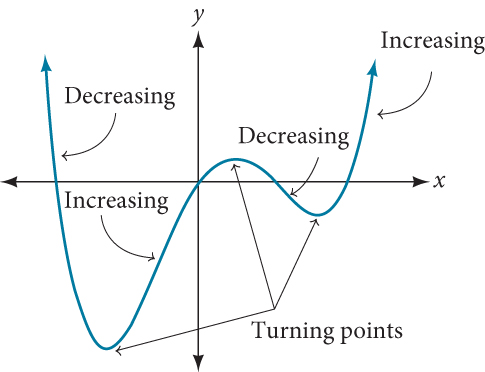
Figure 12
This function[latex]\,f\,[/latex]is a 4th degree polynomial function and has 3 turning points. The maximum number of turning points of a polynomial function is always one less than the degree of the function.
Interpreting Turning Points
A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising). A polynomial of degree[latex]\,n\,[/latex]will have at most[latex]\,n-1\,[/latex]turning points.
EXAMPLE 7
Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function
Find the maximum number of turning points of each polynomial function.
- [latex]\,f\left(x\right)=-{x}^{3}+4{x}^{5}-3{x}^{2}+1[/latex]
- [latex]\,f\left(x\right)=-{\left(x-1\right)}^{2}\left(1+2{x}^{2}\right)[/latex]
Show/Hide Solution
 Solution
Solution
-
First, rewrite the polynomial function in descending order:[latex]\,f\left(x\right)=4{x}^{5}-{x}^{3}-3{x}^{2}+1[/latex]
Identify the degree of the polynomial function. This polynomial function is of degree 5.
The maximum number of turning points is[latex]\,5-1=4.[/latex]
-
First, identify the leading term of the polynomial function if the function were expanded.
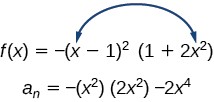
Then, identify the degree of the polynomial function. This polynomial function is of degree 4. The maximum number of turning points is[latex]\,4-1=3.[/latex]
Graphing Polynomial Functions
We can use what we have learned about multiplicities, end behavior, and turning points to sketch graphs of polynomial functions. Let us put this all together and look at the steps required to graph polynomial functions.
How To
Given a polynomial function, sketch the graph.
- Find the intercepts.
- Check for symmetry.
- If the function is an even function, its graph is symmetrical about the[latex]\,y\text{-}[/latex]axis, that is,[latex]\,f\left(-x\right)=f\left(x\right).\,[/latex]
- If a function is an odd function, its graph is symmetrical about the origin, that is,[latex]\,f\left(-x\right)=-f\left(x\right).[/latex]
- Use the multiplicities of the zeros to determine the behavior of the polynomial at the[latex]\,x\text{-}[/latex]intercepts.
- Determine the end behavior by examining the leading term.
- Use the end behavior and the behavior at the intercepts to sketch a graph.
- Ensure that the number of turning points does not exceed one less than the degree of the polynomial.
- Optionally, use technology to check the graph.
EXAMPLE 8
Sketching the Graph of a Polynomial Function
Sketch a graph of[latex]\,f\left(x\right)=-2{\left(x+3\right)}^{2}\left(x-5\right).[/latex]
Show/Hide Solution
 Solution
Solution
This graph has two[latex]\,x\text{-}[/latex]intercepts. At[latex]\,x=-3,\,[/latex]the factor is squared, indicating a multiplicity of 2. The graph will bounce at this[latex]\,x\text{-}[/latex]intercept. At[latex]\,x=5,\,[/latex]the function has a multiplicity of one, indicating the graph will cross through the axis at this intercept.
The[latex]\,y\text{-}[/latex]intercept is found by evaluating[latex]\,f\left(0\right).[/latex]
[latex]\begin{array}{ccc}\hfill f\left(0\right)& =& -2{\left(0+3\right)}^{2}\left(0-5\right)\hfill \\ & =& -2\cdot 9\cdot \left(-5\right)\hfill \\ & =& 90\hfill \end{array}[/latex]
The[latex]\,y\text{-}[/latex]intercept is[latex]\,\left(0,90\right).[/latex]
Additionally, we can see the leading term, if this polynomial were multiplied out, would be[latex]\,-2{x}^{3},\,[/latex]so the end behavior is that of a vertically reflected cubic, with the outputs decreasing as the inputs approach infinity, and the outputs increasing as the inputs approach negative infinity. See Figure 13.
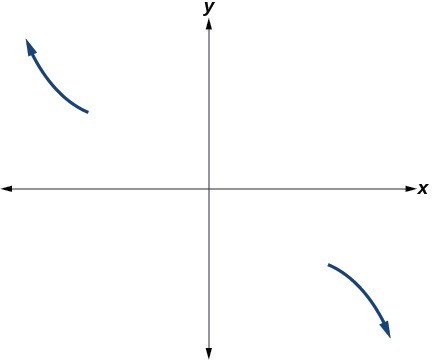
Figure 13
To sketch this, we consider that:
- As[latex]\,x\to -\infty \,[/latex]the function[latex]\,f\left(x\right)\to \infty ,\,[/latex]so we know the graph starts in the second quadrant and is decreasing toward the[latex]\,x\text{-}[/latex]axis.
- Since[latex]\,f\left(-x\right)=-2{\left(-x+3\right)}^{2}\left(-x–5\right)\,[/latex]is not equal to[latex]\,f\left(x\right),\,[/latex]the graph does not display symmetry.
- At[latex]\,\left(-3,0\right),\,[/latex]the graph bounces off of the[latex]\,x\text{-}[/latex]axis, so the function must start increasing.
- At[latex]\,\left(0,90\right),\,[/latex]the graph crosses the[latex]\,y\text{-}[/latex]axis at the[latex]\,y\text{-}[/latex]intercept. See Figure 14.
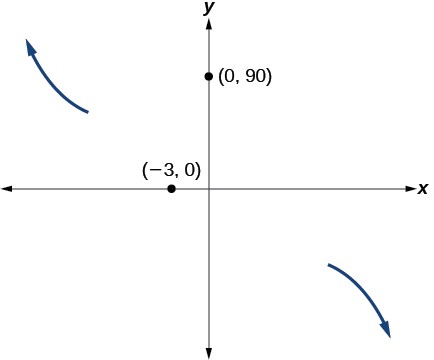
Figure 14
Somewhere after this point, the graph must turn back down or start decreasing toward the horizontal axis because the graph passes through the next intercept at (5,0). See Figure 15.
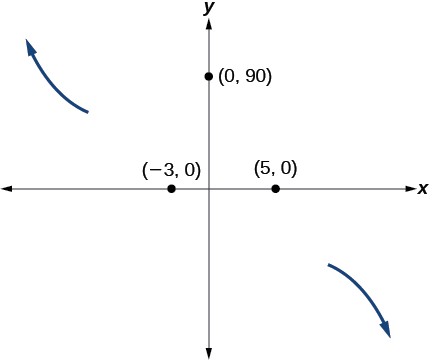
Figure 15
As[latex]\,x\to \infty \,[/latex]the function[latex]\,f\left(x\right)\to \mathrm{-\infty },\,[/latex]so we know the graph continues to decrease, and we can stop drawing the graph in the fourth quadrant.
Using technology, we can create the graph for the polynomial function, shown in Figure 16, and verify that the resulting graph looks like our sketch in Figure 15.
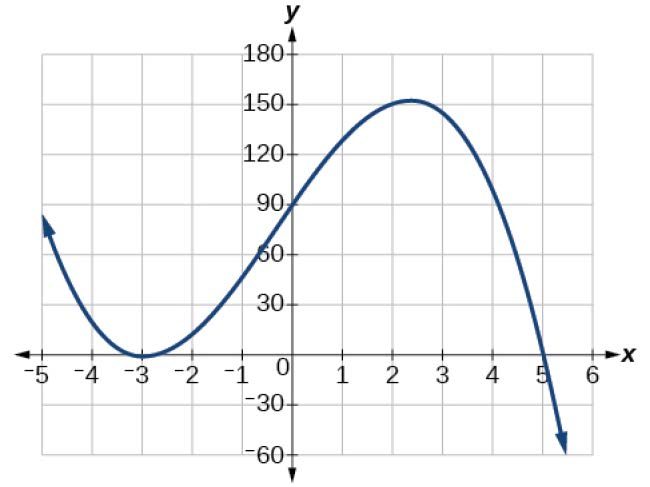
Figure 16 The complete graph of the polynomial function[latex]\,\textcolor{blue}f\left(x\right)=-2{\left(x+3\right)}^{2}\left(x-5\right)[/latex]
 Try It #3
Try It #3
Sketch a graph of[latex]\,f\left(x\right)=\frac{1}{4}x{\left(x-1\right)}^{4}{\left(x+3\right)}^{3}.[/latex]
Using the Intermediate Value Theorem
In some situations, we may know two points on a graph but not the zeros. If those two points are on opposite sides of the[latex]\,x\text{-}[/latex]axis, we can confirm that there is a zero between them. Consider a polynomial function[latex]\,f\,[/latex]whose graph is smooth and continuous. The Intermediate Value Theorem states that for two numbers[latex]\,a\,[/latex]and[latex]\,b\,[/latex]in the domain of[latex]\,f,[/latex]if[latex]\,a[/latex]<[latex]b[/latex] and[latex]f\left(a\right)\ne f\left(b\right),[/latex] then the function[latex]\,f\,[/latex]takes on every value between[latex]\,f\left(a\right)\,[/latex]and[latex]\,f\left(b\right).\,[/latex]
(While the theorem is intuitive, the proof is actually quite complicated and requires higher mathematics.)
We can apply this theorem to a special case that is useful in graphing polynomial functions. If a point on the graph of a continuous function[latex]\,f\,[/latex]at[latex]\,x=a\,[/latex]lies above the[latex]\,x\text{-}[/latex]axis and another point at[latex]\,x=b\,[/latex]lies below the[latex]\,x\text{-}[/latex]axis, there must exist a third point between[latex]\,x=a\,[/latex]and[latex]\,x=b\,[/latex]where the graph crosses the[latex]\,x\text{-}[/latex]axis. Call this point[latex]\,\left(c,\text{ }f\left(c\right)\right).\,[/latex]This means that we are assured there is a solution[latex]\,c\,[/latex]where [latex]f\left(c\right)=0.[/latex]
In other words, the Intermediate Value Theorem tells us that when a polynomial function changes from a negative value to a positive value, the function must cross the[latex]\,x\text{-}[/latex]axis. Figure 10 shows that there is a zero between[latex]\,a\,[/latex]and[latex]\,b.\,[/latex]
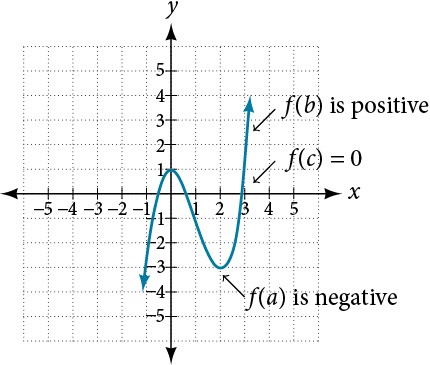
Figure 17 Using the Intermediate Value Theorem to show there exists a zero.
Intermediate Value Theorem
Let[latex]\,f\,[/latex] be a polynomial function. The Intermediate Value Theorem states that if[latex]\,f\left(a\right)\,[/latex] and[latex]\,f\left(b\right)\,[/latex] have opposite signs, then there exists at least one value[latex]\,c\,[/latex] between[latex]\,a\,[/latex] and[latex]\,b\,[/latex] for which[latex]\,f\left(c\right)=0.[/latex]
EXAMPLE 9
Using the Intermediate Value Theorem
Show that the function[latex]\,f\left(x\right)={x}^{3}-5{x}^{2}+3x+6\,[/latex] has at least two real zeros between[latex]\,x=1\,[/latex]and[latex]\,x=4.[/latex]
Show/Hide Solution
 Solution
Solution
As a start, evaluate[latex]\,f\left(x\right)\,[/latex]at the integer values[latex]\,x = 1,2,3,[/latex] and [latex]4.\,[/latex]See Table 2.
Table 2
We see that one zero occurs at[latex]\,x=2.\,[/latex]Also, since[latex]\,f\left(3\right)\,[/latex]is negative and[latex]\,f\left(4\right)\,[/latex]is positive, by the Intermediate Value Theorem, there must be at least one real zero between 3 and 4.
We have shown that there are at least two real zeros between[latex]\,x=1\,[/latex]and[latex]\,x=4.[/latex]
 Analysis
Analysis
We can also see on the graph of the function in Figure 18 that there are two real zeros between[latex]\,x=1\,[/latex]and[latex]\,x=4.[/latex]
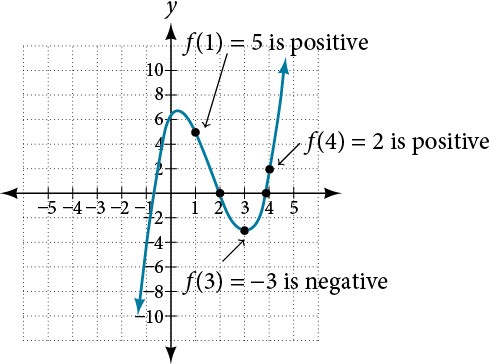 Figure 18
Figure 18
 Try It #4
Try It #4
Show that the function[latex]\,f\left(x\right)=7{x}^{5}-9{x}^{4}-{x}^{2}\,[/latex]has at least one real zero between[latex]\,x=1\,[/latex]and[latex]\,x=2.[/latex]
Writing Formulas for Polynomial Functions
Now that we know how to find zeros of polynomial functions, we can use them to write formulas based on graphs. Because a polynomial function written in factored form will have an[latex]\,x\text{-}[/latex]intercept where each factor is equal to zero, we can form a function that will pass through a set of[latex]\,x\text{-}[/latex]intercepts by introducing a corresponding set of factors.
Factored Form of Polynomials
If a polynomial of lowest degree[latex]\,p\,[/latex]has horizontal intercepts at[latex]\,x={x}_{1},{x}_{2},\dots ,{x}_{n},\,[/latex]then the polynomial can be written in the factored form:
[latex]\,f\left(x\right)=a{\left(x-{x}_{1}\right)}^{{p}_{1}}{\left(x-{x}_{2}\right)}^{{p}_{2}}\cdots {\left(x-{x}_{n}\right)}^{{p}_{n}}\,[/latex]
where the powers[latex]\,{p}_{i}\,[/latex]on each factor can be determined by the behavior of the graph at the corresponding intercept, and the stretch factor[latex]\,a\,[/latex]can be determined given a value of the function other than the[latex]\,x\text{-}[/latex]intercept.
How To
Given a graph of a polynomial function, write a formula for the function.
- Identify the[latex]\,x\text{-}[/latex]intercepts of the graph to find the factors of the polynomial.
- Examine the behavior of the graph at the[latex]\,x\text{-}[/latex]intercepts to determine the multiplicity of each factor.
- Find the polynomial of least degree containing all the factors found in the previous step.
- Use any other point on the graph (the[latex]\,y\text{-}[/latex]intercept may be easiest) to determine the stretch factor.
EXAMPLE 10
Writing a Formula for a Polynomial Function from the Graph
Write a formula for the polynomial function shown in Figure 19.
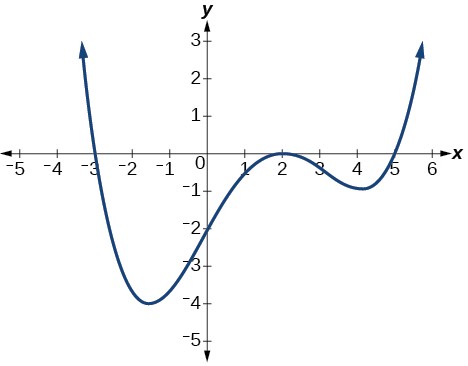
Figure 19
Show/Hide Solution
 Solution
Solution
This graph has three[latex]\,x\text{-}[/latex]intercepts:[latex]\,x=-3,2,\,[/latex]and[latex]\,5.\,[/latex]The[latex]\,y\text{-}[/latex]intercept is located at[latex]\,\left(0,2\right).\,[/latex]At[latex]\,x=-3\,[/latex]and[latex]\,x=5,\,[/latex]the graph passes through the axis linearly, suggesting the corresponding factors of the polynomial will be linear. At[latex]\,x=2,\,[/latex]the graph bounces at the intercept, suggesting the corresponding factor of the polynomial will be second degree (quadratic). Together, this gives us
[latex]f\left(x\right)=a\left(x+3\right){\left(x-2\right)}^{2}\left(x-5\right)[/latex]
To determine the stretch factor, we utilize another point on the graph. We will use the[latex]\,y\text{-}[/latex]intercept[latex]\,\left(0,–2\right),\,[/latex]to solve for[latex]\,a.[/latex]
[latex]\begin{array}{ccc}\hfill f\left(0\right)& =& a\left(0+3\right){\left(0-2\right)}^{2}\left(0-5\right)\hfill \\ \hfill -2& =& a\left(0+3\right){\left(0-2\right)}^{2}\left(0-5\right)\hfill \\ \hfill -2& =& -60a\hfill \\ \hfill a& =& \frac{1}{30}\hfill \end{array}[/latex]
The graphed polynomial appears to represent the function
[latex]\,f\left(x\right)=\frac{1}{30}\left(x+3\right){\left(x-2\right)}^{2}\left(x-5\right).[/latex]
 Try It #5
Try It #5
Given the graph shown in Figure 20, write a formula for the function shown.
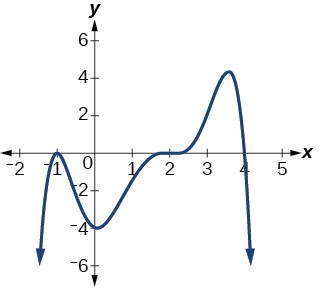
Figure 20
Using Local and Global Extrema
With quadratics, we were able to algebraically find the maximum or minimum value of the function by finding the vertex. For general polynomials, finding these turning points is not possible without more advanced techniques from calculus. Even then, finding where extrema occur can still be algebraically challenging. For now, we will estimate the locations of turning points using technology to generate a graph.
Each turning point represents a local minimum or maximum. Sometimes, a turning point is the highest or lowest point on the entire graph. In these cases, we say that the turning point is a global maximum or a global minimum. These are also referred to as the absolute maximum and absolute minimum values of the function.
Local and Global Extrema
A local maximum or local minimum at[latex]\,x=a\,[/latex](sometimes called the relative maximum or minimum, respectively) is the output at the highest or lowest point on the graph in an open interval around[latex]\,x=a.\,[/latex]If a function has a local maximum at[latex]\,a,\,[/latex]then[latex]\,f\left(a\right)\ge f\left(x\right)\,[/latex]for all[latex]\,x\,[/latex]in an open interval around[latex]\,x=a.\,[/latex]If a function has a local minimum at[latex]\,a,\,[/latex]then[latex]\,f\left(a\right)\le f\left(x\right)\,[/latex]for all[latex]\,x\,[/latex]in an open interval around[latex]\,x=a.[/latex]
A global maximum or global minimum is the output at the highest or lowest point of the function. If a function has a global maximum at [latex]\,a,\,[/latex]then[latex]\,f\left(a\right)\ge f\left(x\right)\,[/latex]for all[latex]\,x.\,[/latex]If a function has a global minimum at[latex]\,a,\,[/latex]then[latex]\,f\left(a\right)\le f\left(x\right)\,[/latex]for all[latex]\,x.[/latex]
We can see the difference between local and global extrema in Figure 21.
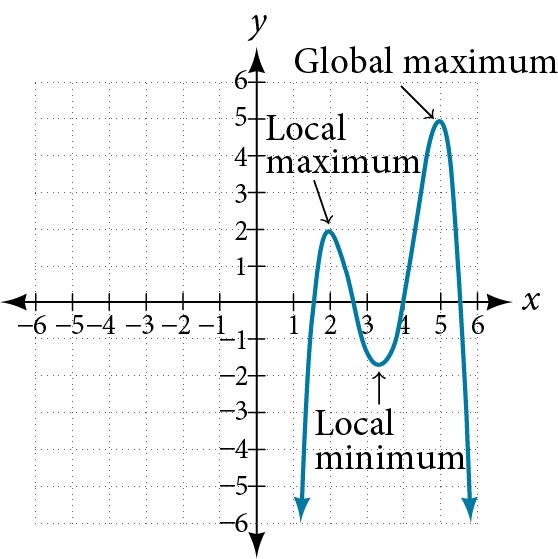
Figure 21
 Q&A
Q&A
Do all polynomial functions have a global minimum or maximum?
No. Only polynomial functions of even degree have a global minimum or maximum. For example,[latex]\,f\left(x\right)=x\,[/latex]has neither a global maximum nor a global minimum.
EXAMPLE 11
Using Local Extrema to Solve Applications
An open-top box is to be constructed by cutting out squares from each corner of a 14 cm by 20 cm sheet of plastic and then folding up the sides. Find the size of squares that should be cut out to maximize the volume enclosed by the box.
Show/Hide Solution
 Solution
Solution
We will start this problem by drawing a picture like that in Figure 22, labeling the width of the cut-out squares with a variable,
Figure 22
Notice that after a square is cut out from each end, it leaves a[latex]\,\left(14-2w\right)\,[/latex]cm by[latex]\,\left(20-2w\right)\,[/latex]cm rectangle for the base of the box, and the box will be[latex]\,w\,[/latex]cm tall. This gives the volume
[latex]\begin{array}{ccc}\hfill V\left(w\right)& =& \left(20-2w\right)\left(14-2w\right)w\hfill \\ & =& 280w-68{w}^{2}+4{w}^{3}\hfill \end{array}[/latex]
Notice, since the factors are[latex]\,w,\,[/latex][latex]\,20–2w\,[/latex]and[latex]\,14–2w,\,[/latex]the three zeros are 10, 7, and 0, respectively. Because a height of 0 cm is not reasonable, we consider the only the zeros 10 and 7. The shortest side is 14 and we are cutting off two squares, so values[latex]\,w\,[/latex]may take on are greater than zero or less than 7. This means we will restrict the domain of this function to 0<[latex]w[/latex]<7. Using technology to sketch the graph of[latex]\,V\left(w\right)\,[/latex]on this reasonable domain, we get a graph like that in Figure 23.
We can use this graph to estimate the maximum value for the volume, restricted to values for[latex]\,w\,[/latex]that are reasonable for this problem—values from 0 to 7.
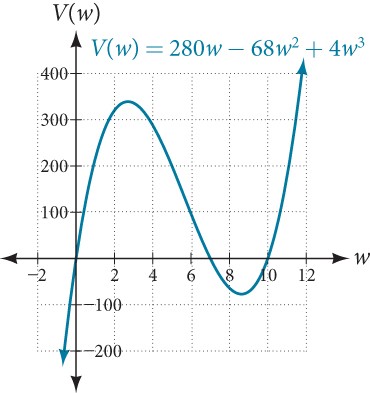
Figure 23
From this graph, we turn our focus to only the portion on the reasonable domain,[latex]\,\left[0,\text{ }7\right].\,[/latex]We can estimate the maximum value to be around 340 cubic cm, which occurs when the squares are about 2.75 cm on each side. To improve this estimate, we could use advanced features of our technology, if available, or simply change our window to zoom in on our graph to produce Figure 24.
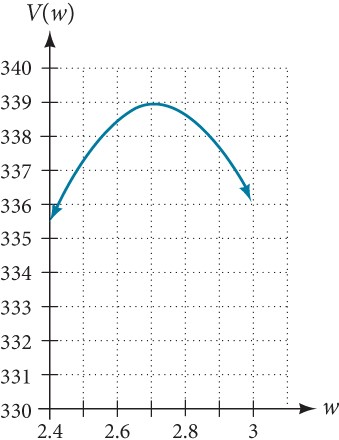
Figure 24
From this zoomed-in view, we can refine our estimate for the maximum volume to about 339 cubic cm, when the squares measure approximately 2.7 cm on each side.
 Try It #6
Try It #6
Use technology to find the maximum and minimum values on the interval[latex]\,\left[-1,4\right]\,[/latex]of the function
[latex]\,f\left(x\right)=-0.2{\left(x-2\right)}^{3}{\left(x+1\right)}^{2}\left(x-4\right).[/latex]
Section 1.1 Part 2 Exercises
[Answers to odd problem numbers are provided at the end of the problem set. Just scroll down!]
Verbal
1. What is the difference between an [latex]x-[/latex]intercept and a zero of a polynomial function [latex]f[/latex]?
2. If a polynomial function of degree [latex]n[/latex] has [latex]n[/latex] distinct zeros, what do you know about the graph of the function?
3. Explain how the Intermediate Value Theorem can assist us in finding a zero of a function.
4. Explain how the factored form of the polynomial helps us in graphing it.
5. If the graph of a polynomial just touches the [latex]x-[/latex]axis and then changes direction, what can we conclude about the factored form of the polynomial?
Algebraic
For the following exercises, find the [latex]x-[/latex] or [latex]t-[/latex]intercepts of the polynomial functions.
6. [latex]\,C\left(t\right)=2\left(t-4\right)\left(t+1\right)\left(t-6\right)[/latex]
7. [latex]\,C\left(t\right)=3\left(t+2\right)\left(t-3\right)\left(t+5\right)[/latex]
8. [latex]\,C\left(t\right)=4t{\left(t-2\right)}^{2}\left(t+1\right)[/latex]
9. [latex]\,C\left(t\right)=2t\left(t-3\right){\left(t+1\right)}^{2}[/latex]
10. [latex]\,C\left(t\right)=2{t}^{4}-8{t}^{3}+6{t}^{2}[/latex]
11. [latex]\,C\left(t\right)=4{t}^{4}+12{t}^{3}-40{t}^{2}[/latex]
12. [latex]\,f\left(x\right)={x}^{4}-{x}^{2}[/latex]
13. [latex]\,f\left(x\right)={x}^{3}+{x}^{2}-20x[/latex]
14. [latex]f\left(x\right)={x}^{3}+6{x}^{2}-7x[/latex]
15. [latex]f\left(x\right)={x}^{3}+{x}^{2}-4x-4[/latex]
16. [latex]f\left(x\right)={x}^{3}+2{x}^{2}-9x-18[/latex]
17. [latex]f\left(x\right)=2{x}^{3}-{x}^{2}-8x+4[/latex]
18. [latex]f\left(x\right)={x}^{6}-7{x}^{3}-8[/latex]
19. [latex]f\left(x\right)=2{x}^{4}+6{x}^{2}-8[/latex]
20. [latex]f\left(x\right)={x}^{3}-3{x}^{2}-x+3[/latex]
21. [latex]f\left(x\right)={x}^{6}-2{x}^{4}-3{x}^{2}[/latex]
22. [latex]f\left(x\right)={x}^{6}-3{x}^{4}-4{x}^{2}[/latex]
23. [latex]f\left(x\right)={x}^{5}-5{x}^{3}+4x[/latex]
For the following exercises, use the Intermediate Value Theorem to confirm that the given polynomial has at least one zero within the given interval.
24. [latex]f\left(x\right)={x}^{3}-9x,\,[/latex] between[latex]\,x=-4\,[/latex]and[latex]\,x=-2.[/latex]
25. [latex]f\left(x\right)={x}^{3}-9x,\,[/latex] between[latex]\,x=2\,[/latex]and[latex]\,x=4.[/latex]
26. [latex]f\left(x\right)={x}^{5}-2x,\,[/latex] between[latex]\,x=1\,[/latex]and[latex]\,x=2.[/latex]
27. [latex]f\left(x\right)=-{x}^{4}+4,\,[/latex] between[latex]\,x=1\,[/latex]and[latex]\,x=3[/latex]
28. [latex]f\left(x\right)=-2{x}^{3}-x,\,[/latex] between[latex]\,x=–1\,[/latex] and[latex]\,x=1.[/latex]
29. [latex]f\left(x\right)={x}^{3}-100x+2,\,[/latex] between[latex]\,x=0.01\,[/latex] and[latex]\,x=0.1[/latex]
For the following exercises, find the zeros and give the multiplicity of each.
30. [latex]f\left(x\right)={\left(x+2\right)}^{3}{\left(x-3\right)}^{2}[/latex]
31. [latex]f\left(x\right)={x}^{2}{\left(2x+3\right)}^{5}{\left(x-4\right)}^{2}[/latex]
32. [latex]f\left(x\right)={x}^{3}{\left(x-1\right)}^{3}\left(x+2\right)[/latex]
33. [latex]f\left(x\right)={x}^{2}\left({x}^{2}+4x+4\right)[/latex]
34. [latex]f\left(x\right)={\left(2x+1\right)}^{3}\left(9{x}^{2}-6x+1\right)[/latex]
35. [latex]f\left(x\right)={\left(3x+2\right)}^{5}\left({x}^{2}-10x+25\right)[/latex]
36. [latex]f\left(x\right)=x\left(4{x}^{2}-12x+9\right)\left({x}^{2}+8x+16\right)[/latex]
37. [latex]f\left(x\right)={x}^{6}-{x}^{5}-2{x}^{4}[/latex]
38. [latex]f\left(x\right)=3{x}^{4}+6{x}^{3}+3{x}^{2}[/latex]
39. [latex]f\left(x\right)=4{x}^{5}-12{x}^{4}+9{x}^{3}[/latex]
40. [latex]f\left(x\right)=2{x}^{4}\left({x}^{3}-4{x}^{2}+4x\right)[/latex]
41. [latex]f\left(x\right)=4{x}^{4}\left(9{x}^{4}-12{x}^{3}+4{x}^{2}\right)[/latex]
Graphical
For the following exercises, graph the polynomial functions. Note [latex]x-[/latex]and [latex]y-[/latex]intercepts, multiplicity, and end behavior.
42. [latex]f\left(x\right)={\left(x+3\right)}^{2}\left(x-2\right)[/latex]
43. [latex]g\left(x\right)=\left(x+4\right){\left(x-1\right)}^{2}[/latex]
44. [latex]h\left(x\right)={\left(x-1\right)}^{3}{\left(x+3\right)}^{2}[/latex]
45. [latex]k\left(x\right)={\left(x-3\right)}^{3}{\left(x-2\right)}^{2}[/latex]
46. [latex]m\left(x\right)=-2x\left(x-1\right)\left(x+3\right)[/latex]
47. [latex]n\left(x\right)=-3x\left(x+2\right)\left(x-4\right)[/latex]
For the following exercises, use the graphs to write the formula for a polynomial function of least degree.
48. 
49. 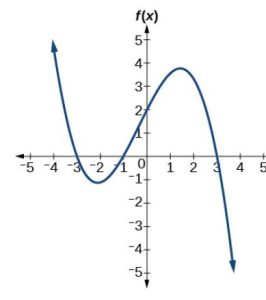
50.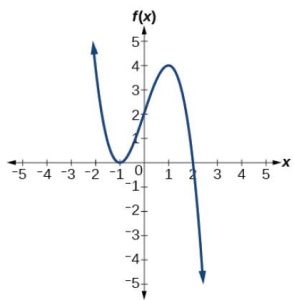
51.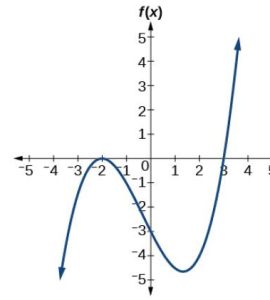
52.
For the following exercises, use the graph to identify zeros and multiplicity.
53. 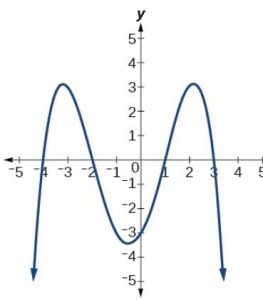
54.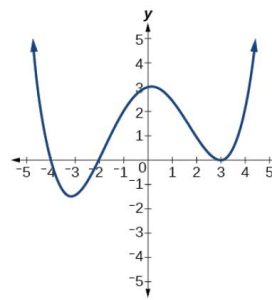
55. 
56.
For the following exercises, use the given information about the polynomial graph to write the equation.
57. Degree 3. Zeros at[latex]\,x=–2,[/latex] [latex]\,x=1,\,[/latex]and[latex]\,x=3.\;\;y-[/latex]intercept at[latex]\,\left(0,–4\right).[/latex]
58. Degree 3. Zeros at[latex]\,x=–5,[/latex] [latex]\,x=–2,\,[/latex]and[latex]\,x=1. \;\;y-[/latex]intercept at[latex]\,\left(0,6\right)[/latex]
59. Degree 5. Roots of multiplicity 2 at[latex]\,x=3\,[/latex] and[latex]\,x=1\,[/latex] and a root of multiplicity 1 at[latex]\,x=–3. \;\;y-[/latex]intercept at[latex]\,\left(0,9\right)[/latex]
60. Degree 4. Root of multiplicity 2 at[latex]\,x=4\,[/latex]and a roots of multiplicity 1 at[latex]\,x=1\,[/latex]and[latex]\,x=–2. \;\;y-[/latex]intercept at[latex]\,\left(0,\text{–}3\right).[/latex]
61. Degree 5. Double zero at[latex]\,x=1\,[/latex]and triple zero at[latex]\,x=3.\,[/latex] Passes through the point[latex]\,\left(2,15\right).[/latex]
62. Degree 3. Zeros at[latex]\,x=4,[/latex][latex]\,x=3,\,[/latex]and[latex]\,x=2. \;\;y-[/latex]intercept at[latex]\,\left(0,-24\right).[/latex]
63. Degree 3. Zeros at[latex]\,x=-3,[/latex][latex]\,x=-2,\,[/latex]and[latex]\,x=1. \;\;y-[/latex]intercept at[latex]\,\left(0,12\right).[/latex]
64. Degree 5. Roots of multiplicity 2 at[latex]\,x=-3\,[/latex]and[latex]\,x=2\,[/latex]and a root of multiplicity 1 at[latex]\,x=-2. \;\;y-[/latex]intercept at[latex]\,\left(0, 4\right).[/latex]
65. Degree 4. Roots of multiplicity 2 at[latex]\,x=\frac{1}{2}\,[/latex]and roots of multiplicity 1 at[latex]\,x=6\,[/latex]and[latex]\,x=-2. \;\; y-[/latex]intercept at[latex]\,\left(0,18\right).[/latex]
66. Double zero at[latex]\,x=-3\,[/latex]and triple zero at[latex]\,x=0.\,[/latex]Passes through the point[latex]\,\left(1,32\right).[/latex]
Technology
For the following exercises, use a calculator to approximate local minima and maxima or the global minimum and maximum.
67. [latex]f\left(x\right)={x}^{3}-x-1[/latex]
68. [latex]f\left(x\right)=2{x}^{3}-3x-1[/latex]
69. [latex]f\left(x\right)={x}^{4}+x[/latex]
70. [latex]f\left(x\right)=-{x}^{4}+3x-2[/latex]
71. [latex]f\left(x\right)={x}^{4}-{x}^{3}+1[/latex]
Extensions
For the following exercises, use the graphs to write a polynomial function of least degree.
72.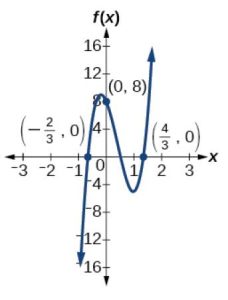
73.
74.
Real-World Applications
For the following exercises, write the polynomial function that models the given situation.
75. A rectangle has a length of 10 units and a width of 8 units. Squares of[latex]\,x\,[/latex] by[latex]\,x\,[/latex] units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a polynomial function in terms of[latex]\,x.[/latex]
76. Consider the same rectangle of the preceding problem. Squares of[latex]\,2x\,[/latex] by[latex]\,2x\,[/latex] units are cut out of each corner. Express the volume of the box as a polynomial in terms of[latex]\,x.[/latex]
77. A square has sides of 12 units. Squares[latex]\,x\text{ }+1\,[/latex]by[latex]\,x\text{ }+1\,[/latex] units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a function in terms of[latex]\,x.[/latex]
78. A cylinder has a radius of[latex]\,x+2\,[/latex] units and a height of 3 units greater. Express the volume of the cylinder as a polynomial function.
79. A right circular cone has a radius of[latex]\,3x+6\,[/latex] and a height 3 units less. Express the volume of the cone as a polynomial function. The volume of a cone is[latex]\,V=\frac{1}{3}\pi {r}^{2}h\,[/latex] for radius[latex]\,r\,[/latex] and height[latex]\,h.[/latex]
Answers to Section 1.1 Part 2 Odd Problems
1. The [latex]x-[/latex]intercept is where the graph of the function crosses the [latex]x-[/latex]axis, and the zero of the function is the input value for which [latex]f\left(x\right)=0[/latex].
3. If we evaluate the function at [latex]a[/latex] and at [latex]b[/latex], and the sign of the function value changes, then we know a zero exists between [latex]a[/latex] and [latex]b[/latex].
5. There will be a factor raised to an even power.
7. [latex]\left(-2,0\right),\left(3,0\right),\left(-5,0\right)[/latex]
9. [latex]\,\left(3,0\right),\left(-1,0\right),\left(0,0\right)[/latex]
11. [latex]\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(2,0\right)[/latex]
13. [latex]\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(4,0\right)[/latex]
15. [latex]\left(2,0\right),\text{ }\left(-2,0\right),\text{ }\left(-1,0\right)[/latex]
17. [latex]\left(-2,0\right),\,\left(2,0\right),\,\left(\frac{1}{2},0\right)[/latex]
19. [latex]\left(1,0\right),\text{ }\left(-1,0\right)[/latex]
21. [latex]\left(0,0\right),\,\left(\sqrt{3},0\right),\,\left(-\sqrt{3},0\right)[/latex]
23. [latex]\left(0,0\right),\text{ }\left(1,0\right)\text{, }\left(-1,0\right),\text{ }\left(2,0\right),\text{ }\left(-2,0\right)[/latex]
25. [latex]f\left(2\right)=–10\,[/latex] and[latex]\,f\left(4\right)=28.[/latex] Sign change confirms.
27. [latex]f\left(1\right)=3\,[/latex]and[latex]\,f\left(3\right)=–77.\,[/latex] Sign change confirms.
29. [latex]f\left(0.01\right)=1.000001\,[/latex] and[latex]\,f\left(0.1\right)=–7.999.\,[/latex] Sign change confirms.
31. 0 with multiplicity 2,[latex]\,-\frac{3}{2}\,[/latex] with multiplicity 5, 4 with multiplicity 2
33. 0 with multiplicity 2, –2 with multiplicity 2
35. [latex]-\frac{2}{3}\,\text{with}\,\text{multiplicity}\,5\text{,}\,5\,\text{with}\,\text{multiplicity}\,\text{2}[/latex]
37.
[latex]\text{0}\,\text{with}\,\text{multiplicity}\,4\text{,}\,2\,\text{with}\,\text{multiplicity}\,1\text{,}\,\text{1}\,\text{with}\,\text{multiplicity}\,1[/latex]
39. with multiplicity 2, 0 with multiplicity 3
41. [latex]\text{0}\,\text{with}\,\text{multiplicity}\,6\text{,}\,\frac{2}{3}\,\text{with}\,\text{multiplicity}\,2[/latex]
43. [latex]x-[/latex]intercepts, [latex]\left(1, 0\right)[/latex] with multiplicity 2, [latex]\left(–4, 0\right)\,[/latex]with multiplicity 1, [latex]y\text{-}[/latex]intercept [latex]\left(0, 4\right).[/latex]
As [latex]\phantom{\rule{0.2em}{0ex}}x\to -\infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to -\infty ,\,\text{as}\phantom{\rule{0.2em}{0ex}}x\to \infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to \infty .[/latex]
45. [latex]x-[/latex]intercepts[latex]\,\left(3,0\right)\,[/latex]with multiplicity 3,[latex]\,\left(2,0\right)\,[/latex]with multiplicity 2,[latex]\,y\text{-}[/latex]intercept[latex]\,\left(0,–108\right).\,[/latex]
As [latex]x\to -\infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to -\infty ,\phantom{\rule{0.2em}{0ex}}\text{as}\phantom{\rule{0.2em}{0ex}}x\to \infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to \infty .[/latex]
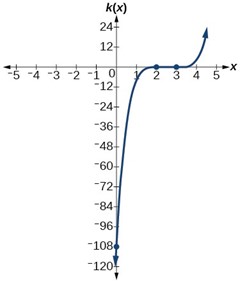
47. [latex]x-[/latex]intercepts[latex]\,\left(0, 0\right),\text{ }\left(–2, 0\right),\text{ }\left(4,0\right)\,[/latex]with multiplicity 1,[latex]\,y\text{-}[/latex]intercept[latex]\,\left(0, 0\right).[/latex]
As [latex]x\to -\infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to \infty ,\phantom{\rule{0.2em}{0ex}}\text{as}\phantom{\rule{0.2em}{0ex}}x\to \infty ,\phantom{\rule{0.2em}{0ex}}f\left(x\right)\to -\infty .[/latex]
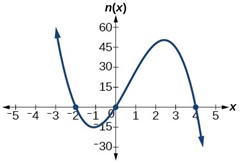
49. [latex]f\left(x\right)=-\frac{2}{9}\left(x-3\right)\left(x+1\right)\left(x+3\right)[/latex]
51. [latex]f\left(x\right)=\frac{1}{4}{\left(x+2\right)}^{2}\left(x-3\right)[/latex]
53. -4, -2, 1, 3 with multiplicity 1
55. -2, 3 each with multiplicity 2
57. [latex]f\left(x\right)=-\frac{2}{3}\left(x+2\right)\left(x-1\right)\left(x-3\right)[/latex]
59. [latex]f\left(x\right)=\frac{1}{3}{\left(x-3\right)}^{2}{\left(x-1\right)}^{2}\left(x+3\right)[/latex]
61. [latex]f\left(x\right)=-15{\left(x-1\right)}^{2}{\left(x-3\right)}^{3}[/latex]
63. [latex]f\left(x\right)=-2\left(x+3\right)\left(x+2\right)\left(x-1\right)[/latex]
65. [latex]f\left(x\right)=-\frac{3}{2}{\left(2x-1\right)}^{2}\left(x-6\right)\left(x+2\right)[/latex]
67. local max[latex]\,\left(–\text{.58, –}.62\right),\,[/latex] local min[latex]\,\left(\text{.58, –1}\text{.38}\right)\,[/latex]
69. global min[latex]\,\left(–\text{.63, –}\text{.47}\right)\,[/latex]
71. global min[latex]\,\text{(}\text{.75, }\text{.89)}[/latex]
73. [latex]f\left(x\right)={\left(x-500\right)}^{2}\left(x+200\right)[/latex]
75. [latex]f\left(x\right)=4{x}^{3}-36{x}^{2}+80x[/latex]
77. [latex]f\left(x\right)=4{x}^{3}-36{x}^{2}+60x+100[/latex]
79. [latex]f\left(x\right)=\pi \left(9{x}^{3}+45{x}^{2}+72x+36\right)[/latex]

 Q&A
Q&A Solution
Solution Try It #1
Try It #1


 Solution
Solution
 Solution
Solution
 Analysis
Analysis  Try It #2
Try It #2

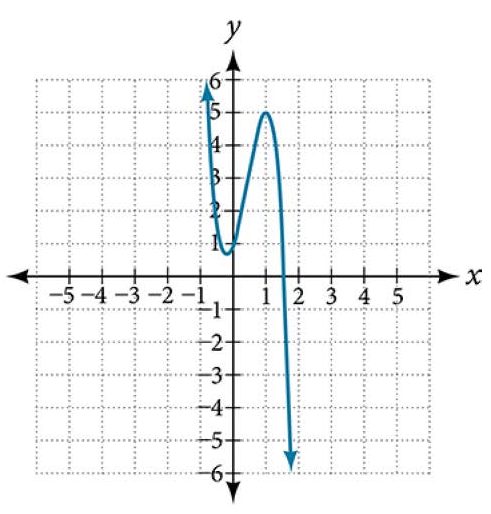





































 Try It #2
Try It #2


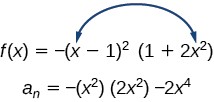




 Try It #3
Try It #3
 Analysis
Analysis Figure 18
Figure 18 Try It #4
Try It #4
 Try It #5
Try It #5

 Q&A
Q&A


 Try It #6
Try It #6














