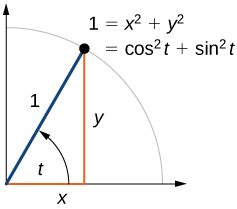Section 1.4: Trigonometric Functions

Section 1.4:  Part 1

This content comes directly from OpenStax’s textbook Algebra and Trigonometry Section 7.2 Right Triangle Trigonometry.

Access this resource for free at https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites

Learning Objectives

In this section you will:

  • Use right triangles to evaluate trigonometric functions.
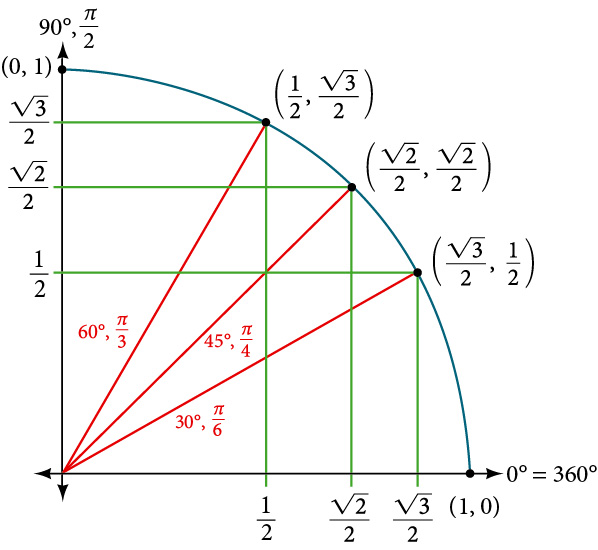
  • Find function values for[latex]\,30°\left(\frac{\pi }{6}\right),45°\left(\frac{\pi }{4}\right),[/latex] and [latex]\,60°\left(\frac{\pi }{3}\right).[/latex]
  • Use equal cofunctions of complementary angles.
  • Use the definitions of trigonometric functions of any angle.
  • Use right-triangle trigonometry to solve applied problems.

Let’s Get Started…

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task. In fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

Using Right Triangles to Evaluate Trigonometric Functions

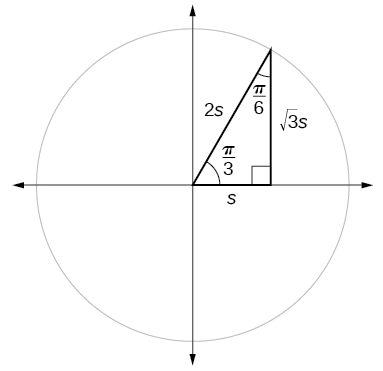
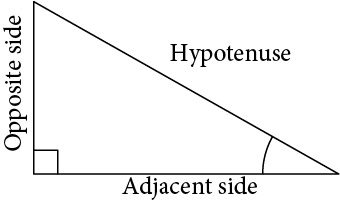
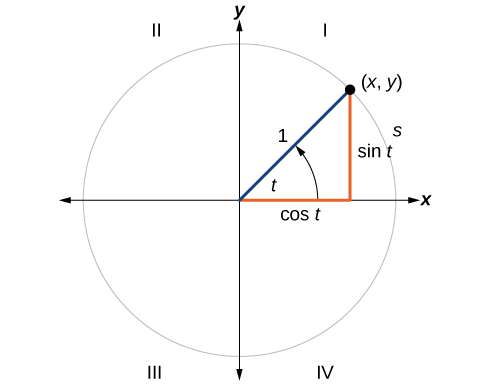
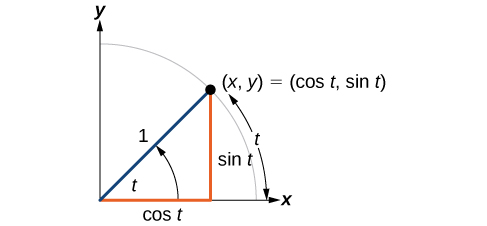
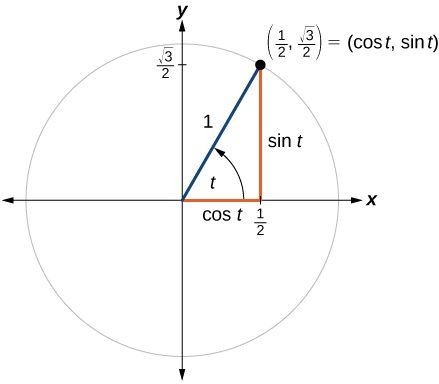
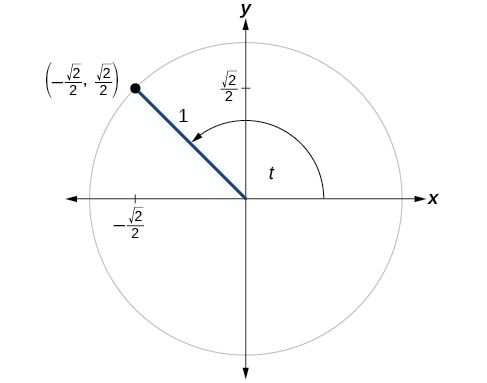
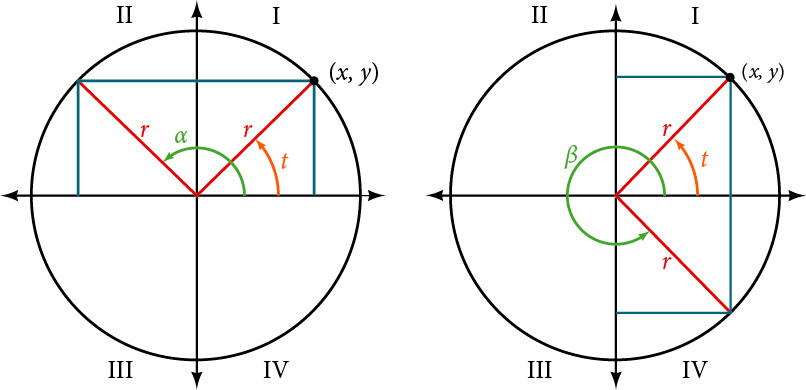
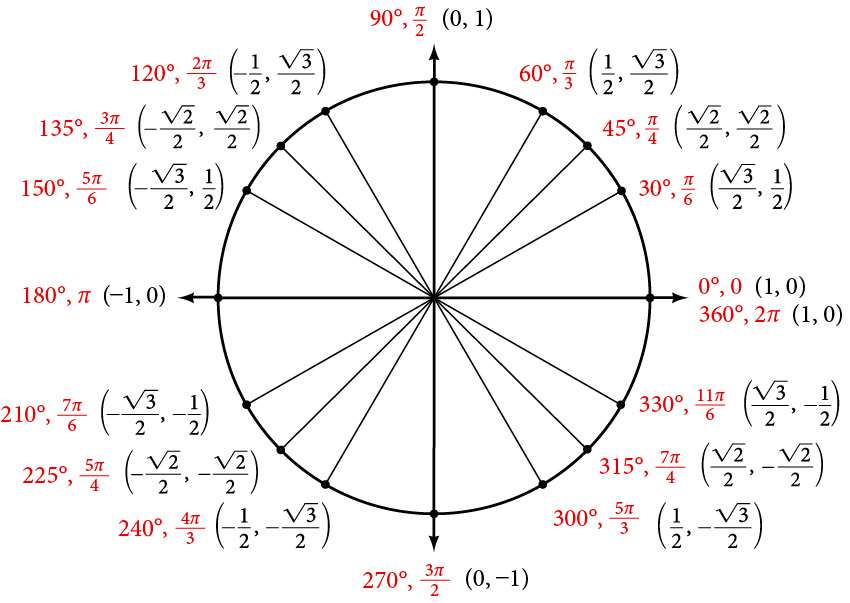
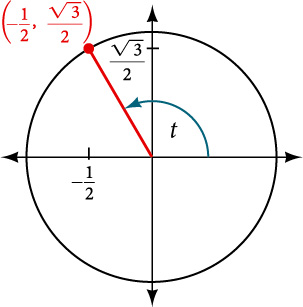
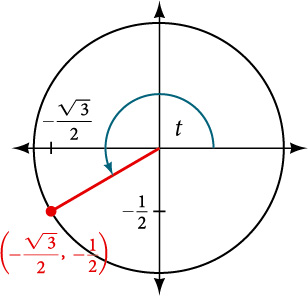
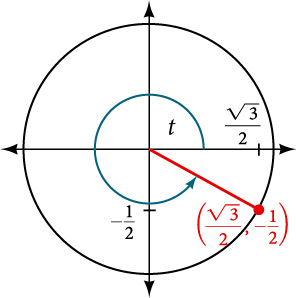
Figure 1 shows a right triangle with a vertical side of length[latex]\,y[/latex] and a horizontal side has length[latex]\,x[/latex].  Notice that the triangle is inscribed in a circle of radius 1. Such a circle, with a center at the origin and a radius of 1, is known as a unit circle.

 

Figure 1

 

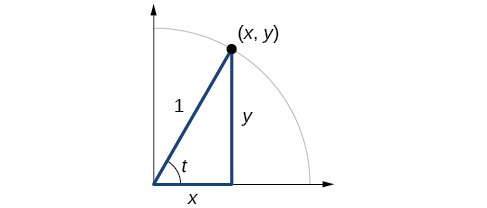
We can define the trigonometric functions in terms an angle[latex]\,t[/latex] and the lengths of the sides of the triangle. The adjacent side,[latex]\,x[/latex], is the side closest to the angle. (Adjacent means “next to.”) The opposite side,[latex]\,y[/latex], is the side across from the angle. The hypotenuse, of length 1, is the side of the triangle opposite the right angle. These sides are labeled in Figure 2.

 

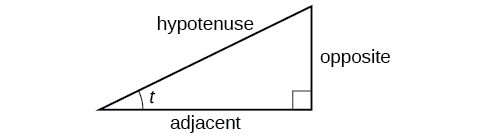
Figure 2 The sides of a right triangle in relation to angle t

 

Given a right triangle with an acute angle of[latex]\,t[/latex], the first three trigonometric functions are listed.

 

[latex]\begin{array}{cccc}\phantom{\rule{2.5em}{0ex}}\text{Sine}\hfill & \phantom{\rule{1em}{0ex}}\text{sin}\left(t\right)\hfill & = &\frac{\text{opposite}}{\text{hypotenuse}}\hfill \end{array}[/latex]

[latex]\begin{array}{cccc}\phantom{\rule{1.5em}{0ex}}\text{Cosine}\hfill & \phantom{\rule{1em}{0ex}}\text{cos}\left(t\right)\hfill & = &\frac{\text{adjacent}}{\text{hypotenuse}}\hfill \end{array}[/latex]

[latex]\begin{array}{cccc}\hfill \text{Tangent}& \phantom{\rule{1em}{0ex}}\text{tan}\left(t\right)\hfill & = & \frac{\text{opposite}}{\text{adjacent}}\hfill \end{array}[/latex]

 

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”

For the triangle shown in Figure 1, we have the following.

[latex]\begin{array}{ccc} \text{sin}\left(t\right) & = & \frac{y}{1} \\ \text{cos}\left(t\right) & = & \frac{x}{1} \\ \text{tan}\left(t\right) & = & \frac{y}{x} \end{array}[/latex]

 

How To

Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle.

  1. Find the sine as the ratio of the opposite side to the hypotenuse.
  2. Find the cosine as the ratio of the adjacent side to the hypotenuse.
  3. Find the tangent as the ratio of the opposite side to the adjacent side.

 

EXAMPLE 1

Evaluating a Trigonometric Function of a Right Triangle

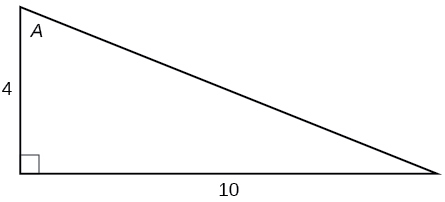
Given the triangle shown in Figure 3, find the value of[latex]\,\mathrm{cos}\,\left(\alpha\right) .[/latex]

 

Figure 3

 

Show/Hide Solution

 

image Try It #1

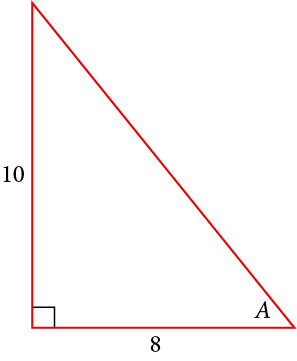
Given the triangle shown in Figure 4, find the value of[latex]\,\text{sin}\,\left(t\right).[/latex]

 

Figure 4

 

Reciprocal Functions

In addition to sine, cosine, and tangent, there are three more functions. These too are defined in terms of the sides of the triangle.

 

[latex]\begin{array}{cccc}\phantom{\rule{2em}{0ex}}\text{Secant}\hfill & \phantom{\rule{1em}{0ex}}\text{sec}\left(t\right)\hfill & = &\frac{\text{hypotenuse}}{\text{adjacent}}\hfill \end{array}[/latex]

[latex]\begin{array}{cccc}\hfill \phantom{\rule{1.3em}{0ex}}\text{Cosecant}& \hfill \phantom{\rule{1em}{0ex}}\text{csc}\left(t\right)& = &\frac{\text{hypotenuse}}{\text{opposite}}\hfill \end{array}[/latex]

[latex]\begin{array}{cccc}\hfill \text{Cotangent}& \phantom{\rule{1em}{0ex}}\text{cot}\left(t\right)& = & \frac{\text{adjacent}}{\text{opposite}}\hfill \end{array}[/latex]

 

Take another look at these definitions. These functions are the reciprocals of the first three functions

 

[latex]\begin{array}{cccccc}\hfill \text{sin}\left(t\right)& =& \frac{1}{\text{csc}\left(t\right)}\hfill & \hfill \phantom{\rule{2em}{0ex}}\text{csc}\left(t\right)& =& \frac{1}{\text{sin}\left(t\right)}\hfill \\ \hfill \text{cos}\left(t\right)& =& \frac{1}{\text{sec}\left(t\right)}\hfill & \hfill \phantom{\rule{2em}{0ex}}\text{sec}\left(t\right)& =& \frac{1}{\text{cos}\left(t\right)}\hfill \\ \hfill \text{tan}\left(t\right)& =& \frac{1}{\text{cot}\left(t\right)}\hfill & \hfill \phantom{\rule{2em}{0ex}}\text{cot}\left(t\right)& =& \frac{1}{\text{tan}\left(t\right)}\hfill \end{array}[/latex]

 

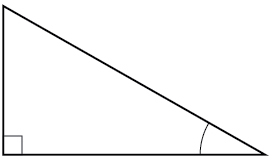
When working with right triangles, keep in mind that the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure 5. The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

 

Figure 5  The side adjacent to one angle is opposite the other angle.

 

Many problems ask for all six trigonometric functions for a given angle in a triangle. A possible strategy to use is to find the sine, cosine, and tangent of the angles first. Then, find the other trigonometric functions easily using the reciprocals.

 

How To

Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles.

  1. If needed, draw the right triangle and label the angle provided.
  2. Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
  3. Find the required function:
    • sine as the ratio of the opposite side to the hypotenuse
    • cosine as the ratio of the adjacent side to the hypotenuse
    • tangent as the ratio of the opposite side to the adjacent side
    • secant as the ratio of the hypotenuse to the adjacent side
    • cosecant as the ratio of the hypotenuse to the opposite side
    • cotangent as the ratio of the adjacent side to the opposite side

 

EXAMPLE 2

Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure 6, evaluate[latex]\,\text{sin}\left(\alpha\right),\,\text{cos}\left(\alpha\right),\,\text{tan}\left(\alpha\right),\,\text{sec}\left(\alpha\right),\,\text{csc}\left(\alpha\right),\,\text{and}\,\text{cot}\left(\alpha\right).[/latex]

 

Figure 6

 

Show/Hide Solution

image Analysis

Another approach would have been to find sine, cosine, and tangent first. Then find their reciprocals to determine the other functions.

 

[latex]\text{sec}\left(\alpha\right) = \frac{1}{\text{cos}\left(\alpha\right)} = \frac{1}{\frac{3}{5}}=\frac{5}{3}[/latex]
[latex]\text{csc}\left(\alpha\right) = \frac{1}{\text{csc}\left(\alpha\right)} = \frac{1}{\frac{4}{5}}=\frac{5}{4}[/latex]
[latex]\text{cot}\left(\alpha\right) = \frac{1}{\text{tan}\left(\alpha\right)} = \frac{1}{\frac{4}{3}}=\frac{3}{4}[/latex]

 

image Try It #2

Using the triangle shown in Figure 7, evaluate[latex]\,\text{sin}\left(t\right),\,\text{cos}\left(t\right),\,\text{tan}\left(t\right),\,\text{sec}\left(t\right),\,\text{csc}\left(t\right),\,\text{and}\,\text{cot}\left(t\right).[/latex]

 

Figure 7

 

Finding Trigonometric Functions of Special Angles Using Side Lengths

It is helpful to evaluate the trigonometric functions as they relate to the special angles—multiples of[latex]\,30°,60°,[/latex]and[latex]\,45°.\,[/latex]Remember, however, that when dealing with right triangles, we are limited to angles between[latex]\,0°\text{ and 90°}\text{.}[/latex]

Suppose we have a[latex]\,30°, 60°, 90°\,[/latex]triangle, which can also be described as a[latex]\,\frac{\pi }{6}, \frac{\pi }{3}, \frac{\pi }{2}\,[/latex]triangle. The sides have lengths in the relation[latex]\,s, \sqrt{3}s, 2s.\,[/latex]

The sides of a[latex]\,45°, 45°, 90°\,[/latex]triangle, which can also be described as a[latex]\,\frac{\pi }{4}, \frac{\pi }{4}, \frac{\pi }{2}\,[/latex]triangle, have lengths in the relation[latex]\,s, s, \sqrt{2}s.\,[/latex]

These relations are shown in Figure 8.

 

Figure 8 Side lengths of special triangles

 

How To

Given trigonometric functions of a special angle, evaluate using side lengths.

  1. Use the side lengths shown in Figure 8 for the special angle you wish to evaluate.
  2. Use the ratio of side lengths appropriate to the function you wish to evaluate.

 

EXAMPLE 3

Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of[latex]\,\frac{\pi }{3},[/latex] using side lengths.

 

Show/Hide Solution

 

image Try It #3

Find the exact value of the trigonometric functions of[latex]\,\frac{\pi }{4},[/latex] using side lengths.

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles, we notice a pattern. In a right triangle with angles of[latex]\,\frac{\pi }{6}\,[/latex] and[latex]\,\frac{\pi }{3}[/latex], we see that the sine of[latex]\,\frac{\pi }{3}[/latex], namely[latex]\,\frac{\sqrt{3}}{2}[/latex], is also the cosine of[latex]\,\frac{\pi }{6}[/latex], while the sine of[latex]\,\frac{\pi }{6}[/latex], namely[latex]\,\frac{1}{2}[/latex], is also the cosine of[latex]\,\frac{\pi }{3}.[/latex]

 

[latex]\begin{array}{cccc}\hfill \mathrm{sin}\left(\frac{\pi }{3}\right)& = &\mathrm{cos}\left(\frac{\pi }{6}\right)\hfill & = &\frac{\sqrt{3}s}{2s}\hfill & = &\frac{\sqrt{3}}{2}\hfill \\ \hfill \mathrm{sin}\left(\frac{\pi }{6}\right)& = &\mathrm{cos}\left(\frac{\pi }{3}\right)\hfill & = &\frac{s}{2s}\hfill & = &\frac{1}{2}\hfill \end{array}[/latex]

See Figure 9.

 

Figure 9

 

This result should not be surprising because, as we see from Figure 9, the side opposite the angle of[latex]\,\frac{\pi }{3}\,[/latex]is also the side adjacent to[latex]\,\frac{\pi }{6},[/latex] so[latex]\,\mathrm{sin}\left(\frac{\pi }{3}\right)\,[/latex]and[latex]\,\mathrm{cos}\left(\frac{\pi }{6}\right)\,[/latex]are exactly the same ratio of the same two sides, [latex]\,\sqrt{3}s\,[/latex] and [latex]\,2s.\,[/latex] Similarly,[latex]\,\mathrm{cos}\left(\frac{\pi }{3}\right)\,[/latex]and[latex]\,\mathrm{sin}\left(\frac{\pi }{6}\right)\,[/latex]are also the same ratio using the same two sides, [latex]\,s\,[/latex] and[latex]\,2s.[/latex]

The interrelationship between the sines and cosines of[latex]\,\frac{\pi }{6}\,[/latex] and[latex]\,\frac{\pi }{3}\,[/latex] also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to[latex]\,\pi ,[/latex]and the right angle is[latex]\,\frac{\pi }{2},[/latex] the remaining two angles must also add up to[latex]\,\frac{\pi }{2}.\,[/latex]That means that a right triangle can be formed with any two angles that add to[latex]\,\frac{\pi }{2}\,[/latex]—in other words, any two complementary angles. So we may state a cofunction identity: If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure 10.

 

Figure 10 Cofunction identity of sine and cosine of complementary angles

 

Using this identity, we can state without calculating, for instance, that the sine of[latex]\,\frac{\pi }{12}\,[/latex] equals the cosine of[latex]\,\frac{5\pi }{12},[/latex] and that the sine of[latex]\,\frac{5\pi }{12}\,[/latex] equals the cosine of[latex]\,\frac{\pi }{12}.\,[/latex] We can also state that if, for a given angle[latex]\,t, \mathrm{cos}\left(t\right)=\frac{5}{13},[/latex] then[latex]\,\mathrm{sin}\left(\frac{\pi }{2}-t\right)=\frac{5}{13}\,[/latex] as well.

 

Cofunction Identities

The cofunction identities in radians are listed in Table 1.

[latex]\mathrm{cos}\left(t\right)=\mathrm{sin}\left(\frac{\pi }{2}-t\right)[/latex] [latex]\mathrm{sin}\left(t\right)=\mathrm{cos}\left(\frac{\pi }{2}-t\right)[/latex]
[latex]\mathrm{tan}\left(t\right)=\mathrm{cot}\left(\frac{\pi }{2}-t\right)[/latex] [latex]\mathrm{cot}\left(t\right)=\mathrm{tan}\left(\frac{\pi }{2}-t\right)[/latex]
[latex]\mathrm{sec}\left(t\right)=\mathrm{csc}\left(\frac{\pi }{2}-t\right)[/latex] [latex]\mathrm{csc}\left(t\right)=\mathrm{sec}\left(\frac{\pi }{2}-t\right)[/latex]
Table 1

 

How To

Given the sine and cosine of an angle, find the sine or cosine of its complement.

  1. To find the sine of the complementary angle, find the cosine of the original angle.
  2. To find the cosine of the complementary angle, find the sine of the original angle.

 

EXAMPLE 4

Using Cofunction Identities

If[latex]\,\mathrm{sin}\left(t\right)=\frac{5}{12},[/latex] find[latex]\,\mathrm{cos}\left(\frac{\pi }{2}-t\right).[/latex]

 

Show/Hide Solution

 

Try It #4

If[latex]\,\mathrm{csc}\,\left(\frac{\pi }{6}\right)=2,[/latex] find[latex]\,\mathrm{sec}\,\left(\frac{\pi }{3}\right).[/latex]

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

 

How To

Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.

  1. For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
  2. Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
  3. Using the value of the trigonometric function and the known side length, solve for the missing side length.

 

EXAMPLE 5

Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure 11.

 

Figure 11

 

Show/Hide Solution

 

image Try It #5

A right triangle has one angle of[latex]\,\frac{\pi }{3}\,[/latex]and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

Using Right Triangle Trigonometry to Solve Applied Problems

Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height.

Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. See Figure 12.

 

Figure 12

 

How To

Given a tall object, measure its height indirectly.

  1. Make a sketch of the problem situation to keep track of known and unknown information.
  2. Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
  3. At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
  4. Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
  5. Solve the equation for the unknown height.

 

EXAMPLE 6

Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57º between a line of sight to the top of the tree and the ground, as shown in Figure 13. Find the height of the tree.

 

Figure 13

 

Show/Hide Solution

 

image Try It #6

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of[latex]\,\frac{5\pi }{12}\,[/latex]with the ground? Round to the nearest foot.

Section 1.4 Part 1 Exercises

[Answers to odd problem numbers are provided at the end of the problem set.  Just scroll down!]

[Part 2 about The Unit Circle follows!]

Verbal

1. For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.


2. When a right triangle with a hypotenuse of 1 is placed in a circle of radius 1, which sides of the triangle correspond to the x– and y-coordinates?

 

3. The tangent of an angle compares which sides of the right triangle?

 

4. What is the relationship between the two acute angles in a right triangle?

 

5. Explain the cofunction identity.

 

Algebraic

For the following exercises, use cofunctions of complementary angles.

 

6. [latex]\mathrm{cos}\left(34°\right)=\mathrm{sin}\left(\_\_\_°\right)[/latex]

 

7. [latex]\mathrm{cos}\left(\frac{\pi }{3}\right)=\mathrm{sin}\left(\_\_\_\right)[/latex]

 

8. [latex]\mathrm{csc}\left(21°\right)=\mathrm{sec}\left(\_\_\_°\right)[/latex]

 

9. [latex]\mathrm{tan}\left(\frac{\pi }{4}\right)=\mathrm{cot}\left(\_\_\_\right)[/latex]

 

For the following exercises, find the lengths of the missing sides if side [latex]\,a[/latex] is opposite angle [latex]\,A[/latex] side [latex]\,b[/latex]is opposite angle [latex]\,B[/latex] and side [latex]\,c[/latex] is the hypotenuse.

 

10. [latex]\mathrm{cos}\left(\,B\right)=\frac{4}{5},a=10[/latex]

 

11. [latex]\mathrm{sin}\left(\,B\right)=\frac{1}{2},a=20[/latex]

 

12. [latex]\mathrm{tan}\left(\,A\right)=\frac{5}{12},b=6[/latex]

 

13. [latex]\mathrm{tan}\left(\,A\right)=100,b=100[/latex]

 

14. [latex]\mathrm{sin}\left(\,B\right)=\frac{1}{\sqrt{3}},a=2[/latex]

 

15. [latex]a=5,\measuredangle \,A=60°[/latex]

 

16. [latex]c=12,\measuredangle \,A=45°[/latex]

 

Graphical

For the following exercises, use Figure 14 to evaluate each trigonometric function of angle [latex]\,A.[/latex]

Figure 14

 

17. [latex]\mathrm{sin}\left(\,A\right)[/latex]

 

18. [latex]\mathrm{cos}\left(\,A\right)[/latex]

 

19. [latex]\mathrm{tan}\left(\,A\right)[/latex]

 

20. [latex]\mathrm{csc}\left(\,A\right)[/latex]

 

21. [latex]\mathrm{sec}\left(\,A\right)[/latex]

 

22. [latex]\mathrm{cot}\left(\,A\right)[/latex]

 

For the following exercises, use Figure 15 to evaluate each trigonometric function of angle [latex]\,A.[/latex]

 

Figure 15

23. [latex]\mathrm{sin}\left(\,A\right)[/latex]

 

24. [latex]\mathrm{cos}\left(\,A\right)[/latex]

 

25. [latex]\mathrm{tan}\left(\,A\right)[/latex]

 

26. [latex]\mathrm{csc}\left(\,A\right)[/latex]

 

27. [latex]\mathrm{sec}\left(\,A\right)[/latex]

 

28. [latex]\mathrm{cot}\left(\,A\right)[/latex]

 

For the following exercises, solve for the unknown sides of the given triangle.

 

29.

 

30.

 

31.

 

Technology

For the following exercises, use a calculator to find the length of each side to four decimal places.

32.

 

33.

 

34.

 

35.

 

36.

 

37. [latex]b=15,\measuredangle \,B=15°[/latex]

 

38. [latex]c=200,\measuredangle \,B=5°[/latex]

 

39. [latex]c=50,\measuredangle \,B=21°[/latex]

 

40. [latex]a=30,\measuredangle \,A=27°[/latex]

 

41. [latex]b=3.5,\measuredangle \,A=78°[/latex]

 

Extensions

42. Find[latex]\,x.[/latex]

 

43. Find[latex]\,x.[/latex]

 

44. Find[latex]\,x.[/latex]

 

45. Find[latex]\,x.[/latex]

 

46.  A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is 36º, and that the angle of depression to the bottom of the tower is 23º. How tall is the tower?

 

47. A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is 43º, and that the angle of depression to the bottom of the tower is 31º. How tall is the tower?

 

48. A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is 15º, and that the angle of depression to the bottom of the monument is 2º. How far is the person from the monument?

 

49. A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is 18º, and that the angle of depression to the bottom of the monument is 3º. How far is the person from the monument?

 

50. There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be 40º. From the same location, the angle of elevation to the top of the antenna is measured to be 43º. Find the height of the antenna.

 

51. There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be 36º. From the same location, the angle of elevation to the top of the lightning rod is measured to be 38º. Find the height of the lightning rod.

 

Real-World Applications

52. A 33-ft ladder leans against a building so that the angle between the ground and the ladder is 80º. How high does the ladder reach up the side of the building?

 

53. A 23-ft ladder leans against a building so that the angle between the ground and the ladder is 80º. How high does the ladder reach up the side of the building?

 

54. The angle of elevation to the top of a building in Charlotte is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.

 

55. The angle of elevation to the top of a building in Seattle is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.

 

56. Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be 60º, how far from the base of the tree am I?

 

 

Answers to Section 1.4 Part 1 Odd Problems

1.

 

3. The tangent of an angle is the ratio of the opposite side to the adjacent side.

 

5. For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.

 

7. [latex]\frac{\pi }{6}[/latex]

 

9. [latex]\frac{\pi }{4}[/latex]

 

11. [latex]b=\frac{20\sqrt{3}}{3},c=\frac{40\sqrt{3}}{3}[/latex]

 

13. [latex]a=10,000, c=10,00.5[/latex]

 

15. [latex]b=\frac{5\sqrt{3}}{3},c=\frac{10\sqrt{3}}{3}[/latex]

 

17. [latex]\frac{5\sqrt{29}}{29}[/latex]

 

19. [latex]\frac{5}{2}[/latex]

 

21. [latex]\frac{\sqrt{29}}{2}[/latex]

 

23. [latex]\frac{5\sqrt{41}}{41}[/latex]

 

25. [latex]\frac{5}{4}[/latex]

 

27. [latex]\frac{\sqrt{41}}{4}[/latex]

 

29. [latex]c=14,b=7\sqrt{3}[/latex]

 

31. [latex]a=15,b=15[/latex]

 

33. [latex]b=9.9970,c=12.2041[/latex]

 

35. [latex]a=2.0838,b=11.8177[/latex]

 

37. [latex]a=55.9808,c=57.9555[/latex]

 

39. [latex]a=46.6790,b=17.9184[/latex]

 

41. [latex]a=16.4662,c=16.8341[/latex]

 

43. 188.3159

 

45. 200.6737

 

47. 498.3471 ft

 

49. 1060.09 ft

 

51. 27.372 ft

 

53. 22.6506 ft

 

55. 368.7633 ft

 

Section 1.4:  Part 2

This content comes directly from OpenStax’s textbook Algebra and Trigonometry Section 7.3 The Unit Circle.

Access this resource for free at https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites

Learning Objectives

In this section you will:

  • Find function values for the sine and cosine of[latex]\,30°\text{ or }\left(\frac{\pi }{6}\right),45°\text{ or }\left(\frac{\pi }{4}\right),[/latex]and[latex]\,{60}^{\circ }\text{ or }\left(\frac{\pi }{3}\right).[/latex]
  • Identify the domain and range of sine and cosine functions.
  • Find reference angles.
  • Use reference angles to evaluate trigonometric functions.

    Let’s Get Started…

    Figure 1 The Singapore Flyer was the world’s tallest Ferris wheel until being overtaken by the High Roller in Las Vegas and the Ain Dubai in Dubai. (credit: ʺVibin JKʺ/Flickr)

    Looking for a thrill? Then consider a ride on the Ain Dubai, the world’s tallest Ferris wheel. Located in Dubai, the most populous city and the financial and tourism hub of the United Arab Emirates, the wheel soars to 820 feet, about 1.5 tenths of a mile. Described as an observation wheel, riders enjoy spectacular views of the Burj Khalifa (the world’s tallest building) and the Palm Jumeirah (a human-made archipelago home to over 10,000 people and 20 resorts) as they travel from the ground to the peak and down again in a repeating pattern. In this section, we will examine this type of revolving motion around a circle. To do so, we need to define the type of circle first, and then place that circle on a coordinate system. Then we can discuss circular motion in terms of the coordinate pairs.

    Finding Trigonometric Functions Using the Unit Circle

    We have already defined the trigonometric functions in terms of right triangles. In this section, we will redefine them in terms of the unit circle. Recall that a unit circle is a circle centered at the origin with radius 1, as shown in Figure 2. The angle (in radians) that[latex]\,t\,[/latex]intercepts forms an arc of length[latex]\,s.\,[/latex]Using the formula[latex]\,s=rt,[/latex] and knowing that[latex]\,r=1,[/latex] we see that for a unit circle,[latex]\,s=t.[/latex]

    The[latex]\,x[/latex]– and[latex]\,y[/latex]–axes divide the coordinate plane into four quarters called quadrants. We label these quadrants to mimic the direction a positive angle would sweep. The four quadrants are labeled I, II, III, and IV.

    For any angle[latex]\,t,[/latex] we can label the intersection of the terminal side and the unit circle as by its coordinates,[latex]\,\left(x,y\right).\,[/latex]The coordinates[latex]\,x\,[/latex]and[latex]\,y\,[/latex]will be the outputs of the trigonometric functions[latex]\,f\left(t\right)=\mathrm{cos}\left(t\,\right)[/latex] and[latex]\,f\left(t\right)=\mathrm{sin}\left(t\,\right)[/latex] respectively. This means[latex]\phantom{\rule{0.3em}{0ex}}x=\text{cos}\left(t\right)\phantom{\rule{0.3em}{0ex}}[/latex] and[latex]\phantom{\rule{0.3em}{0ex}}y=\text{sin}\left(t\right).[/latex]

     

    Figure 2 Unit circle where the central angle is [latex]\,t\,[/latex] radians

     

    Unit Circle

    A unit circle has a center at[latex]\,\left(0,0\right)\,[/latex]and radius[latex]\,1.\,[/latex]In a unit circle, the length of the intercepted arc is equal to the radian measure of the central angle[latex]\,t.[/latex]

    Let[latex]\,\left(x,y\right)\,[/latex]be the endpoint on the unit circle of an arc of arc length[latex]\,s.\,[/latex]The[latex]\,\left(x,y\right)\,[/latex]coordinates of this point can be described as functions of the angle.

     

    Defining Sine and Cosine Functions from the Unit Circle

    The sine function relates a real number[latex]\,t\,[/latex]to the[latex]\,y[/latex]-coordinate of the point where the corresponding angle intercepts the unit circle. More precisely, the sine of an angle[latex]\,t\,[/latex]equals the[latex]\,y[/latex]-value of the endpoint on the unit circle of an arc of length[latex]\,t.\,[/latex]In Figure 2, the sine is equal to[latex]\,y.\,[/latex]Like all functions, the sine function has an input and an output. Its input is the measure of the angle; its output is the[latex]\,y[/latex]-coordinate of the corresponding point on the unit circle.

    The cosine function of an angle[latex]\,t\,[/latex]equals the[latex]\,x[/latex]-value of the endpoint on the unit circle of an arc of length[latex]\,t.\,[/latex]In Figure 3, the cosine is equal to[latex]\,x.[/latex]

     

    Figure 3

     

    Because it is understood that sine and cosine are functions, we do not always need to write them with parentheses:[latex]\,\mathrm{sin}\,t\,[/latex]is the same as[latex]\,\mathrm{sin}\left(t\right)\,[/latex]and[latex]\,\mathrm{cos}\,t\,[/latex]is the same as[latex]\,\mathrm{cos}\left(t\right).\,[/latex]Likewise,[latex]\,{\mathrm{cos}}^{2}t\,[/latex]is a commonly used shorthand notation for[latex]\,{\left(\mathrm{cos}\left(t\right)\right)}^{2}.\,[/latex]Be aware that many calculators and computers do not recognize the shorthand notation. When in doubt, use the extra parentheses when entering calculations into a calculator or computer.

     

    Sine and Cosine Functions

    If[latex]\,t\,[/latex]is a real number and a point[latex]\,\left(x,y\right)\,[/latex]on the unit circle corresponds to a central angle[latex]\,t,[/latex]then

    [latex]\mathrm{cos}\left(t\right)=x[/latex]
    [latex]\mathrm{sin}\left(t\right)=y[/latex]
    sint=y

     

    How To

    Given a point P[latex]\,\left(x,y\right)\,[/latex]on the unit circle corresponding to an angle of[latex]\,t,[/latex] find the sine and cosine.

    1. The sine of[latex]\,t\,[/latex]is equal to the y-coordinate of point[latex]\,P:\text{sin}\left(t\right)=y.[/latex]
    2. The cosine of[latex]\,t\,[/latex]is equal to the x-coordinate of point[latex]\,P:\text{cos}\left(t\right)=x.[/latex]
    P:cost=x.

     

    EXAMPLE 1

    Finding Function Values for Sine and Cosine

    Point[latex]\,P\,[/latex]is a point on the unit circle corresponding to an angle of[latex]\,t,[/latex] as shown in Figure 4. Find[latex]\,\mathrm{cos}\left(t\right)\,[/latex]and[latex]\,\text{sin}\left(t\right).[/latex]

     

    Figure 4

     

    Show/Hide Solution

     

    image Try It #1

    A certain angle[latex]\,t\,[/latex]corresponds to a point on the unit circle at[latex]\,\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\,[/latex]as shown in Figure 5. Find[latex]\,\mathrm{cos}\,\left(t\right)\,[/latex]and[latex]\,\mathrm{sin}\,\left(t\right).[/latex]

     

    Figure 5

     

    Finding Sines and Cosines of Angles on an Axis

    For quadrantral angles, the corresponding point on the unit circle falls on the[latex]\,x[/latex]– or[latex]\,y[/latex]-axis. In that case, we can easily calculate cosine and sine from the values of[latex]\,x\,[/latex]and[latex]\,y.[/latex]

     

    EXAMPLE 2

    Calculating Sines and Cosines along an Axis

    Find[latex]\,\text{cos}\left(90°\right)\,[/latex]and[latex]\,\text{sin}\left(90°\right).[/latex]

     

    Show/Hide Solution

     

    image Try It #2

    Find cosine and sine of the angle [latex]\,\pi .[/latex]

    The Pythagorean Identity

    Now that we can define sine and cosine, we will learn how they relate to each other and the unit circle. Recall that the equation for the unit circle is[latex]\,{x}^{2}+{y}^{2}=1.\,[/latex]Because[latex]\,x=\mathrm{cos}\,\left(t\right)\,[/latex]and[latex]\, y=\mathrm{sin}\,\left(t\right),[/latex] we can substitute for[latex]\,x\,[/latex]and[latex]\,y\,[/latex]to get[latex]\,{\mathrm{cos}}^{2}\left(t\right)+{\mathrm{sin}}^{2}\left(t\right)=1.\,[/latex]This equation,[latex]\,{\mathrm{cos}}^{2}\left(t\right)+{\mathrm{sin}}^{2}\left(t\right)=1,[/latex] is known as the Pythagorean Identity. See Figure 7.

     

    Figure 7

     

    We can use the Pythagorean Identity to find the cosine of an angle if we know the sine, or vice versa. However, because the equation yields two solutions, we need additional knowledge of the angle to choose the solution with the correct sign. If we know the quadrant where the angle is, we can easily choose the correct solution.

     

    Pythagorean Identity

    The Pythagorean Identity states that, for any real number[latex]\,t,[/latex]

    [latex]{\mathrm{cos}}^{2}\left(t\right)+{\mathrm{sin}}^{2}\left(t\right)=1[/latex]

     

    How To

    Given the sine of some angle[latex]\,t\,[/latex]and its quadrant location, find the cosine of[latex]\left(t\right).[/latex]

    1. Substitute the known value of[latex]\,\mathrm{sin}\left(t\,\right)[/latex] into the Pythagorean Identity.
    2. Solve for[latex]\,\mathrm{cos}\left(t\right).[/latex]
    3. Choose the solution with the appropriate sign for the[latex]\,x[/latex]-values in the quadrant where[latex]\,t\,[/latex]is located.

     

    EXAMPLE 3

    Finding a Cosine from a Sine or a Sine from a Cosine

    If[latex]\,\mathrm{sin}\left(t\right)=\frac{3}{7}\,[/latex]and[latex]\,t\,[/latex]is in the second quadrant, find[latex]\,\mathrm{cos}\left(t\right).[/latex]

     

    Show/Hide Solution

     

    image Try It #3

    If[latex]\,\mathrm{cos}\left(t\right)=\frac{24}{25}\,[/latex]and[latex]\,t\,[/latex]is in the fourth quadrant, find[latex]\,\text{sin}\left(t\right).[/latex]

    Finding Sines and Cosines of Special Angles

    We have already learned some properties of the special angles, such as the conversion from radians to degrees, and we found their sines and cosines using right triangles. We can also calculate sines and cosines of the special angles using the Pythagorean Identity.

    Finding Sines and Cosines of[latex]\,45°\,[/latex]Angles

    First, we will look at angles of[latex]\,45°\,[/latex]or[latex]\,\frac{\pi }{4},[/latex] as shown in Figure 9. A[latex]\,45°–45°–90°\,[/latex]triangle is an isosceles triangle, so the[latex]\,x[/latex]– and[latex]\,y[/latex]-coordinates of the corresponding point on the circle are the same. Because the[latex]\,x[/latex]– and[latex]\,y[/latex]-values are the same, the sine and cosine values will also be equal.

     

    Figure 9

     

    At[latex]\,t=\frac{\pi }{4},[/latex] which is 45 degrees, the radius of the unit circle bisects the first quadrantal angle. This means the radius lies along the line[latex]\,y=x.\,[/latex]A unit circle has a radius equal to 1 so the right triangle formed below the line[latex]\,y=x\,[/latex]has sides[latex]\,x\,[/latex]and[latex]\,y\text{ }\left(y=x\right),[/latex] and radius = 1. See Figure 10.

     

    Figure 10

     

    From the Pythagorean Theorem we get

     

    [latex]{x}^{2}+{y}^{2}=1[/latex]

     

    We can then substitute[latex]\,y=x.[/latex]

     

    [latex]{x}^{2}+{x}^{2}=1[/latex]

     

    Next we combine like terms.

    [latex]2{x}^{2}=1[/latex]

     

    And solving for[latex]\,x,[/latex]we get

     

    [latex]\begin{array}{ccc}\hfill {x}^{2}& =& \frac{1}{2}\hfill \\ \hfill x& =& ±\frac{1}{\sqrt{2}}\hfill \end{array}[/latex]

     

    In quadrant I,[latex]\,x=\frac{1}{\sqrt{2}}.[/latex]

     

    At[latex]\,t=\frac{\pi }{4}\,[/latex]or 45 degrees,

    [latex]\begin{array}{cccc}\hfill \left(x,y\right)& =& \left(x,x\right)& =& \left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\hfill & \\ \hfill x& =& \frac{1}{\sqrt{2}}, & y & =& \frac{1}{\sqrt{2}}\hfill \\ \hfill \text{cos}\left(t\right)& =& \frac{1}{\sqrt{2}}, & \text{sin}\left(t\right)& =& \frac{1}{\sqrt{2}}\hfill \end{array}[/latex]

     

    If we then rationalize the denominators, we get

     

    [latex]\begin{array}{ccc}\hfill \text{cos}\left(t\right)& =& \frac{1}{\sqrt{2}}\frac{\sqrt{2}}{\sqrt{2}} \\& =& \frac{\sqrt{2}}{2}\hfill \\ & & & \\ \text{sin}\left(t\right)& =& \frac{1}{\sqrt{2}}\frac{\sqrt{2}}{\sqrt{2}}\hfill \\ & =& \frac{\sqrt{2}}{2}\hfill \end{array}[/latex]

     

    Therefore, the[latex]\,\left(x,y\right)\,[/latex]coordinates of a point on a circle of radius[latex]\,1\,[/latex]at an angle of[latex]\,45°\,[/latex]are[latex]\,\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right).[/latex]

     

    Finding Sines and Cosines of[latex]\,30°\,[/latex]and[latex]\,60°\,[/latex]Angles

    Next, we will find the cosine and sine at an angle of[latex]\,30°,[/latex] or[latex]\,\frac{\pi }{6}.\,[/latex]First, we will draw a triangle inside a circle with one side at an angle of[latex]\,30°,[/latex] and another at an angle of[latex]\,-30°,[/latex] as shown in Figure 11. If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be[latex]\,60°,[/latex] as shown in Figure 12.

     

    Figure 11

     

    Figure 12

     

    Because all the angles are equal, the sides are also equal. The vertical line has length[latex]\,2y,[/latex] and since the sides are all equal, we can also conclude that[latex]\,r=2y\,[/latex]or[latex]\,y=\frac{1}{2}r.\,[/latex]Since[latex]\,\mathrm{sin}\left(t\right)=y,[/latex]

     

    [latex]\mathrm{sin}\left(\frac{\pi }{6}\right)=\frac{1}{2}r[/latex]

     

    And since[latex]\,r=1\,[/latex]in our unit circle,

     

    [latex]\begin{array}{ccc}\hfill \mathrm{sin}\left(\frac{\pi }{6}\right)& =& \frac{1}{2}\left(1\right)\hfill \\ & =& \frac{1}{2}\end{array}[/latex]

     

    Using the Pythagorean Identity, we can find the cosine value.

    [latex]\begin{array}{cccc}\hfill {\mathrm{cos}}^{2}\left(\frac{\pi }{6}\right)+{\mathrm{sin}}^{2}\left(\frac{\pi }{6}\right)& =& 1\hfill & \\ \hfill {\mathrm{cos}}^{2}\left(\frac{\pi }{6}\right)+{\left(\frac{1}{2}\right)}^{2}& =& 1\hfill & \\ \hfill {\mathrm{cos}}^{2}\left(\frac{\pi }{6}\right)& =& \frac{3}{4}\hfill & \phantom{\rule{1em}{0ex}}\text{Use the square root property}.\hfill \\ \hfill \mathrm{cos}\left(\frac{\pi }{6}\right)& =& \frac{±\sqrt{3}}{±\sqrt{4}}=\frac{\sqrt{3}}{2}\hfill & \phantom{\rule{1em}{0ex}}\text{Since }y\text{ is positive, choose the positive root}.\hfill \end{array}[/latex]

    The[latex]\,\left(x,y\right)\,[/latex]coordinates for the point on a circle of radius[latex]\,1\,[/latex]at an angle of[latex]\,30°\,[/latex]are[latex]\,\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right).\,[/latex]At[latex]\,t=\frac{\pi }{3}\text{ (60°}\text{),}[/latex]the radius of the unit circle, 1, serves as the hypotenuse of a 30-60-90 degree right triangle,[latex]\,BAD,[/latex] as shown in Figure 13.

    Angle[latex]\,A\,[/latex]has measure[latex]\,60°.\,[/latex]At point[latex]\,B,[/latex] we draw an angle[latex]\,ABC\,[/latex]with measure of[latex]\,60°.\,[/latex]We know the angles in a triangle sum to[latex]\,180°,[/latex] so the measure of angle[latex]\,C\,[/latex]is also[latex]\,60°.\,[/latex]Now we have an equilateral triangle. Because each side of the equilateral triangle[latex]\,ABC\,[/latex] is the same length, and we know one side is the radius of the unit circle, all sides must be of length 1.

     

    Figure 13

     

    The measure of angle[latex]\,ABD\,[/latex]is 30°. Angle[latex]\,ABC\,[/latex]is double angle[latex]\,ABD,[/latex] so its measure is 60°.[latex]\,BD\,[/latex]is the perpendicular bisector of[latex]\,AC,[/latex] so it cuts[latex]\,AC\,[/latex]in half. This means that[latex]\,AD\,[/latex]is[latex]\,\frac{1}{2}\,[/latex]the radius, or[latex]\,\frac{1}{2}.\,[/latex]Notice that[latex]\,AD\,[/latex]is the[latex]\,x[/latex]-coordinate of point[latex]\,B,[/latex] which is at the intersection of the 60° angle and the unit circle. This gives us a triangle[latex]\,BAD\,[/latex]with hypotenuse of 1 and side[latex]\,x\,[/latex]of length[latex]\,\frac{1}{2}.[/latex]

    From the Pythagorean Theorem, we get

     

    [latex]{x}^{2}+{y}^{2}=1[/latex]

     

    Substituting[latex]\,x=\frac{1}{2},[/latex]we get

     

    [latex]{\left(\frac{1}{2}\right)}^{2}+{y}^{2}=1[/latex]

     

    Solving for[latex]\,y,[/latex]we get

     

    [latex]\begin{array}{ccc}\hfill \frac{1}{4}+{y}^{2}& =& 1\hfill \\ \hfill {y}^{2}& =& 1-\frac{1}{4}\hfill \\ \hfill {y}^{2}& =& \frac{3}{4}\hfill \\ \hfill y& =& ±\frac{\sqrt{3}}{2}\hfill \end{array}[/latex]

     

    Since[latex]\,t=\frac{\pi }{3}\,[/latex]has the terminal side in quadrant I where the[latex]\,y[/latex]–coordinate is positive, we choose[latex]\,y=\frac{\sqrt{3}}{2},[/latex] the positive value.

     

    At[latex]\,t=\frac{\pi }{3}\,[/latex](60°), the[latex]\,\left(x,y\right)\,[/latex]coordinates for the point on a circle of radius[latex]\,1\,[/latex]at an angle of[latex]\,60°\,[/latex] are[latex]\,\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right),[/latex] so we can find the sine and cosine.

    [latex]\begin{array}{cccc}\hfill \left(x,y\right)& =& \left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\hfill & \\ \hfill x& =& \frac{1}{2}, & y& =& \frac{\sqrt{3}}{2}\hfill \\ \hfill \text{cos }\left(t\right)& =& \frac{1}{2}, & \text{ sin }\left(t\right)& =& \frac{\sqrt{3}}{2}\hfill \end{array}[/latex]

    We have now found the cosine and sine values for all of the most commonly encountered angles in the first quadrant of the unit circle. Table 1 summarizes these values.

     

    Angle 0 [latex]\frac{\pi }{6}[/latex] or 30º [latex]\frac{\pi }{4}[/latex] or 45º [latex]\frac{\pi }{3}[/latex] or 60º [latex]\frac{\pi }{2}[/latex] or 90º
    Cosine 1 [latex]\frac{\sqrt{3}}{2}[/latex] [latex]\frac{\sqrt{2}}{2}[/latex] [latex]\frac{1}{2}[/latex] 0
    Sine 0 [latex]\frac{1}{2}[/latex] [latex]\frac{\sqrt{2}}{2}[/latex] [latex]\frac{\sqrt{3}}{2}[/latex] 1
    Table 1 Common angles in the first quadrant of the unit circle.

     

    Figure 14 shows the common angles in the first quadrant of the unit circle.

     

    Figure 14

     

    Using a Calculator to Find Sine and Cosine

    To find the cosine and sine of angles other than the special angles, we turn to a computer or calculator. Be aware: Most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When we evaluate[latex]\,\mathrm{cos}\left(30\right)\,[/latex]on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.

     

    How To

    Given an angle in radians, use a graphing calculator to find the cosine.

    1. If the calculator has degree mode and radian mode, set it to radian mode.
    2. Press the COS key.
    3. Enter the radian value of the angle and press the close-parentheses key “)”.
    4. Press ENTER.

     

    EXAMPLE 4

    Using a Graphing Calculator to Find Sine and Cosine

    Evaluate[latex]\,\mathrm{cos}\left(\frac{5\pi }{3}\right)\,[/latex]using a graphing calculator or computer.

     

    Show/Hide Solution

     

    image Analysis

    We can find the cosine or sine of an angle in degrees directly on a calculator with degree mode. For calculators or software that use only radian mode, we can find the sine of 20º, for example, by including the conversion factor to radians as part of the input:

    [latex]\text{SIN}(\text{ 20 }×\text{ }\pi \text{ }÷\text{ 180 ) ENTER}[/latex]

     

    image Try It #4

    Evaluate[latex]\,\mathrm{sin}\left(\frac{\pi }{3}\right).[/latex]

    Identifying the Domain and Range of Sine and Cosine Functions

    Now that we can find the sine and cosine of an angle, we need to discuss their domains and ranges. What are the domains of the sine and cosine functions? That is, what are the smallest and largest numbers that can be inputs of the functions? Because angles smaller than[latex]\,0\,[/latex]and angles larger than[latex]\,2\pi \,[/latex]can still be graphed on the unit circle and have real values of[latex]\,x,y,\text{and}\,r,[/latex]there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive[latex]\,x[/latex]-axis, and that may be any real number.

    What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We can see the answers by examining the unit circle, as shown in Figure 15. The bounds of the[latex]\,x[/latex]-coordinate are[latex]\,\left[-1,1\right].\,[/latex]The bounds of the[latex]\,y[/latex]-coordinate are also[latex]\,\left[-1,1\right].\,[/latex]Therefore, the range of both the sine and cosine functions is[latex]\,\left[-1,1\right].[/latex]

     

    Figure 15

     

    Finding Reference Angles

    We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the[latex]\,y[/latex]-coordinate on the unit circle, the other angle with the same sine will share the same[latex]\,y[/latex]-value, but have the opposite[latex]\,x[/latex]-value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.

    Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same[latex]\,x[/latex]-value but will have the opposite[latex]\,y[/latex]-value. Therefore, its sine value will be the opposite of the original angle’s sine value.

    As shown in Figure 16, angle[latex]\,\alpha \,[/latex]has the same sine value as angle[latex]\,t;[/latex] the cosine values are opposites. Angle[latex]\,\beta \,[/latex]has the same cosine value as angle[latex]\,t;[/latex] the sine values are opposites.

     

    [latex]\begin{array}{ccc}\mathrm{sin}\left(t\right)=\mathrm{sin}\left(\alpha \right)\hfill & \phantom{\rule{1em}{0ex}}\text{and}\phantom{\rule{1em}{0ex}}& \mathrm{cos}\left(t\right)=-\mathrm{cos}\left(\alpha \right)\hfill \\ \mathrm{sin}\left(t\right)=-\mathrm{sin}\left(\beta \right)\hfill & \phantom{\rule{1em}{0ex}}\text{and}\phantom{\rule{1em}{0ex}}& \mathrm{cos}\left(t\right)=\mathrm{cos}\left(\beta \right)\hfill \end{array}[/latex]

     

    Figure 16

     

    Recall that an angle’s reference angle is the acute angle,[latex]\,t,[/latex] formed by the terminal side of the angle[latex]\,t\,[/latex]and the horizontal axis. A reference angle is always an angle between[latex]\,0\,[/latex]and[latex]\,90°,[/latex] or[latex]\,0\,[/latex]and[latex]\,\frac{\pi }{2}\,[/latex]radians. As we can see from Figure 17, for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

     

    Figure 17

     

    How To

    Given an angle between[latex]\,0\,[/latex]and[latex]\,2\pi,[/latex] find its reference angle.

    1. An angle in the first quadrant is its own reference angle.
    2. For an angle in the second or third quadrant, the reference angle is[latex]\,|\pi -t|\,[/latex]or[latex]\,|180°-t|.[/latex]
    3. For an angle in the fourth quadrant, the reference angle is[latex]\,2\pi -t\,[/latex]or[latex]\,360°-t.[/latex]
    4. If an angle is less than[latex]\,0\,[/latex]or greater than[latex]\,2\pi ,[/latex]add or subtract[latex]\,2\pi \,[/latex]as many times as needed to find an equivalent angle between[latex]\,0\,[/latex]and[latex]\,2\pi .[/latex]
    2π.

     

    EXAMPLE 5

    Finding a Reference Angle

    Find the reference angle of[latex]\,225°\,[/latex]as shown in Figure 18.

     

    Figure 18

     

    Show/Hide Solution

     

    image Try It #5

    Find the reference angle of[latex]\,\frac{5\pi }{3}.[/latex]

    Using Reference Angles

    Now let’s take a moment to reconsider the Ferris wheel introduced at the beginning of this section. Suppose a rider snaps a photograph while stopped twenty feet above ground level. The rider then rotates three-quarters of the way around the circle. What is the rider’s new elevation? To answer questions such as this one, we need to evaluate the sine or cosine functions at angles that are greater than 90 degrees or at a negative angle. Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find[latex]\,\left(x,y\right)\,[/latex]coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies.

    Using Reference Angles to Evaluate Trigonometric Functions

    We can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. The absolute values of the cosine and sine of an angle are the same as those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the[latex]\,x[/latex]-values in that quadrant. The sine will be positive or negative depending on the sign of the[latex]\,y[/latex]-values in that quadrant.

    Using Reference Angles to Find Cosine and Sine

    Angles have cosines and sines with the same absolute value as their reference angles. The sign (positive or negative) can be determined from the quadrant of the angle.

     

    How To

    Given an angle in standard position, find the reference angle, and the cosine and sine of the original angle.

    1. Measure the angle between the terminal side of the given angle and the horizontal axis. That is the reference angle.
    2. Determine the values of the cosine and sine of the reference angle.
    3. Give the cosine the same sign as the[latex]\,x[/latex]-values in the quadrant of the original angle.
    4. Give the sine the same sign as the[latex]\,y[/latex]-values in the quadrant of the original angle.

     

    EXAMPLE 6

    Using Reference Angles to Find Sine and Cosine

    1. Using a reference angle, find the exact value of[latex]\,\mathrm{cos}\left(150°\right)\,[/latex]and[latex]\,\text{sin}\left(150°\right).[/latex]
    1. Using the reference angle, find[latex]\,\mathrm{cos}\,\left(\frac{5\pi }{4}\right)\,[/latex]and[latex]\,\mathrm{sin}\left(\,\frac{5\pi }{4}\right).[/latex]

     

    Show/Hide Solution

     

    image Try It #6

    1. Use the reference angle of[latex]\,315°\,[/latex]to find [latex]\,\mathrm{cos}\left(315°\right)\,[/latex]and[latex]\,\mathrm{sin}\left(315°\right).[/latex]
    1. Use the reference angle of[latex]\,-\frac{\pi }{6}\,[/latex]to find[latex]\,\mathrm{cos}\left(-\frac{\pi }{6}\right)\,[/latex]and[latex]\,\mathrm{sin}\left(-\frac{\pi }{6}\right).[/latex]

    Using Reference Angles to Find Coordinates

    Now that we have learned how to find the cosine and sine values for special angles in the first quadrant, we can use symmetry and reference angles to fill in cosine and sine values for the rest of the special angles on the unit circle. They are shown in Figure 19. Take time to learn the[latex]\,\left(x,y\right)\,[/latex] coordinates of all of the major angles in the first quadrant.

     

    Figure 19 Special angles and coordinates of corresponding points on the unit circle

     

    In addition to learning the values for special angles, we can use reference angles to find[latex]\,\left(x,y\right)\,[/latex]coordinates of any point on the unit circle, using what we know of reference angles along with the identities

    [latex]\begin{array}{c}x=\text{cos}\left(t\right)\hfill \\ y=\text{sin}\left(t\right)\hfill \end{array}[/latex]

    First we find the reference angle corresponding to the given angle. Then we take the sine and cosine values of the reference angle, and give them the signs corresponding to the[latex]\,y[/latex]– and[latex]\,x[/latex]-values of the quadrant.

     

    How To

    Given the angle of a point on a circle and the radius of the circle, find the[latex]\,\left(x,y\right)\,[/latex]coordinates of the point.

    1. Find the reference angle by measuring the smallest angle to the[latex]\,x[/latex]-axis.
    2. Find the cosine and sine of the reference angle.
    3. Determine the appropriate signs for[latex]\,x\,[/latex]and[latex]\,y\,[/latex]in the given quadrant.

     

    EXAMPLE 7

    Using the Unit Circle to Find Coordinates

    Find the coordinates of the point on the unit circle at an angle of[latex]\,\frac{7\pi }{6}.[/latex]

     

    Show/Hide Solution

     

    image Try It #7

    Find the coordinates of the point on the unit circle at an angle of[latex]\,\frac{5\pi }{3}.[/latex]

    Section 1.4 Part 2 Exercises

    [Answers to odd problem numbers are provided at the end of the problem set.  Just scroll down!]

    Verbal

    1. Describe the unit circle.

     

    2. What do the [latex]x-[/latex] and [latex]y-[/latex]coordinates of the points on the unit circle represent?

     

    3. Discuss the difference between a coterminal angle and a reference angle.

     

    4. Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.

     

    5. Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.

     

    Algebraic

    For the following exercises, use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by[latex]\,t\,[/latex]lies. 

    6. [latex]\text{sin}\left(t\right)<0\,[/latex]and[latex]\,\text{cos}\left(t\right)<0[/latex]   7. [latex]\text{sin}\left(t\right)>0\,[/latex]and[latex]\,\mathrm{cos}\left(t\right)>0[/latex]

     

    8. [latex]\text{sin}\left(t\right)>0\,[/latex]and[latex]\,\mathrm{cos}\left(t\right)<0[/latex]

     

    9. [latex]\text{sin}\left(t\right)>0\,[/latex]and[latex]\,\mathrm{cos}\left(t\right)>0[/latex]

     

    For the following exercises, find the exact value of each trigonometric function.

    10.  [latex]\mathrm{sin}\left(\frac{\pi }{2}\right)[/latex]

     

    11. [latex]\mathrm{sin}\left(\frac{\pi }{3}\right)[/latex]

     

    12. [latex]\mathrm{cos}\left(\frac{\pi }{2}\right)[/latex]

     

    13. [latex]\mathrm{cos}\left(\frac{\pi }{3}\right)[/latex]

     

    14. [latex]\mathrm{sin}\left(\frac{\pi }{4}\right)[/latex]

     

    15. [latex]\mathrm{cos}\left(\frac{\pi }{4}\right)[/latex]

     

    16. [latex]\mathrm{sin}\left(\frac{\pi }{6}\right)[/latex]

     

    17. [latex]\mathrm{sin}\left(\pi\right)[/latex]

     

    18. [latex]\mathrm{sin}\left(\frac{3\pi }{2}\right)[/latex]

     

    19. [latex]\mathrm{cos}\left(\pi\right)[/latex]

     

    20. [latex]\mathrm{cos}\left(0\right)[/latex]

     

    21. [latex]\mathrm{cos}\left(\frac{\pi }{6}\right)[/latex]

     

    22. [latex]\mathrm{sin}\left(0\right)[/latex]

     

    Numeric

    For the following exercises, state the reference angle for the given angle.

     

    23. 240º

     

    24. –170º

     

    25. 100º

     

    26. –315º

     

    27. 135º

     

    28. [latex]\frac{5\pi }{4}[/latex]

     

    29. [latex]\frac{2\pi }{3}[/latex]

     

    30. [latex]\frac{5\pi }{6}[/latex]

     

    31. [latex]\frac{-11\pi }{3}[/latex]

     

    32. [latex]\frac{-7\pi }{4}[/latex]

     

    33. [latex]\frac{-\pi }{8}[/latex]

     

    For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.

    34. 225º

     

    35. 300º

     

    36. 320º

     

    37. 135º

     

    38. 210º

     

    39. 120º

     

    40. 250º

     

    41. 150º

     

    42. [latex]\frac{5\pi }{4}[/latex]

     

    43. [latex]\frac{7\pi }{6}[/latex]

     

    44. [latex]\frac{5\pi }{3}[/latex]

     

    45.[latex]\frac{3\pi }{4}[/latex]

     

    46. [latex]\frac{4\pi }{3}[/latex]

     

    47. [latex]\frac{2\pi }{3}[/latex]

     

    48. [latex]\frac{5\pi }{6}[/latex]

     

    49. [latex]\frac{7\pi }{4}[/latex]

     

    For the following exercises, find the requested value.

     

    50. If[latex]\,\text{cos}\left(t\right)=\frac{1}{7}\,[/latex]and[latex]\,t\,[/latex]is in the fourth quadrant, find[latex]\,\text{sin}\left(t\right).[/latex]

     

    51. If[latex]\,\text{cos}\left(t\right)=\frac{2}{9}\,\,[/latex]and[latex]\,t\,[/latex]is in the first quadrant, find[latex]\,\text{sin}\left(t\right).[/latex]

     

    52. If[latex]\,\text{sin}\left(t\right)=\frac{3}{8}\,[/latex]and[latex]\,t\,[/latex]is in the second quadrant, find[latex]\,\text{cos}\left(t\right).[/latex]

     

    53. If[latex]\,\text{sin}\left(t\right)=-\frac{1}{4}\,[/latex]and[latex]\,t\,[/latex]is in the third quadrant, find[latex]\,\text{cos}\left(t\right).[/latex]

     

    54. Find the coordinates of the point on a circle with radius 15 corresponding to an angle of 220º.

     

    55. Find the coordinates of the point on a circle with radius 20 corresponding to an angle of 120º.

     

    56. Find the coordinates of the point on a circle with radius 8 corresponding to an angle of[latex]\,\frac{7\pi }{4}.[/latex]

     

    57. Find the coordinates of the point on a circle with radius 16 corresponding to an angle of[latex]\,\frac{5\pi }{9}.[/latex]

     

    58. State the domain of the sine and cosine functions.

     

    59. State the range of the sine and cosine functions.

     

    Graphical

    For the following exercises, use the given point on the unit circle to find the value of the sine and cosine of[latex]\,t.[/latex]

    60.

     

    61.

     

    62.

     

    63

    64.

    65.

    66.
    67.
    68.
    69.
    70.
    71.
    72.
    73.
    74.
    75.
    76.
    77.
    78.
    79.

    Technology

    For the following exercises, use a graphing calculator to evaluate.

    80. [latex]\mathrm{sin}\,\left(\frac{5\pi }{9}\right)[/latex]

     

    81. [latex]\mathrm{cos}\,\left(\frac{5\pi }{9}\right)[/latex]

     

    82. [latex]\mathrm{sin}\,\left(\frac{\pi }{10}\right)[/latex]

     

    83. [latex]\mathrm{cos}\,\left(\frac{\pi }{10}\right)[/latex]

     

    84. [latex]\mathrm{sin}\,\left(\frac{3\pi }{4}\right)[/latex]

     

    85. [latex]\mathrm{cos}\,\left(\frac{3\pi }{4}\right)[/latex]

     

    86. [latex]\mathrm{sin}\,\left(98°\right)[/latex]

     

    87. [latex]\mathrm{cos}\,\left(98°\right)[/latex]

     

    88. [latex]\mathrm{cos}\,\left(310°\right)[/latex]

     

    89. [latex]\mathrm{sin}\,\left(310°\right)[/latex]

     

    Extensions

    For the following exercises, evaluate.

    90. [latex]\mathrm{sin}\left(\frac{11\pi }{3}\right)\,\mathrm{cos}\left(\frac{-5\pi }{6}\right)[/latex]

     

    91. [latex]\mathrm{sin}\left(\frac{3\pi }{4}\right)\,\mathrm{cos}\left(\frac{5\pi }{3}\right)[/latex]

     

    92. [latex]\mathrm{sin}\left(-\frac{4\pi }{3}\right)\,\mathrm{cos}\left(\frac{\pi }{2}\right)[/latex]

     

    93. [latex]\mathrm{sin}\left(\frac{-9\pi }{4}\right)\,\mathrm{cos}\left(\frac{-\pi }{6}\right)[/latex]

     

    94. [latex]\mathrm{sin}\left(\frac{\pi }{6}\right)\,\mathrm{cos}\left(\frac{-\pi }{3}\right)[/latex]

     

    95. [latex]\mathrm{sin}\left(\frac{7\pi }{4}\right)\mathrm{cos}\left(\frac{-2\pi }{3}\right)[/latex]

     

    96. [latex]\mathrm{cos}\left(\frac{5\pi }{6}\right)\,\mathrm{cos}\left(\frac{2\pi }{3}\right)[/latex]

     

    97. [latex]\mathrm{cos}\left(\frac{-\pi }{3}\right)\mathrm{cos}\left(\frac{\pi }{4}\right)[/latex]

     

    98. [latex]\mathrm{sin}\left(\frac{-5\pi }{4}\right)\,\mathrm{sin}\left(\frac{11\pi }{6}\right)[/latex]

     

    99. [latex]\mathrm{sin}\left(\pi \right)\mathrm{sin}\left(\frac{\pi }{6}\right)[/latex]

     

    Real-World Applications

    For the following exercises, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point (0, 1), that is, on the due north position. Assume the carousel revolves counter clockwise.

    100. What are the coordinates of the child after 45 seconds?

     

    101. What are the coordinates of the child after 90 seconds?

     

    102. What are the coordinates of the child after 125 seconds?

     

    103.  When will the child have coordinates[latex]\,\left(0.707,–0.707\right)\,[/latex]if the ride lasts 6 minutes? (There are multiple answers.)

     

    104. When will the child have coordinates[latex]\,\left(–0.866,–0.5\right)\,[/latex] if the ride lasts 6 minutes?

     

    Answers to Section 1.4 Part 2 Odd Problems

    1. The unit circle is a circle of radius 1 centered at the origin.

     

    3. Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, [latex]\,t,[/latex] formed by the terminal side of the angle [latex]\,t,[/latex] and the horizontal axis.

     

    5.The sine values are equal.

     

    7. I

     

    9. IV

     

    11. [latex]\frac{\sqrt{3}}{2}[/latex]

     

    13. [latex]\frac{1}{2}[/latex]

     

    15. [latex]\frac{\sqrt{2}}{2}[/latex]

     

    17.  0

     

    19.  -1

     

    21.  [latex]\frac{\sqrt{3}}{2}[/latex]

     

    23. 60°

     

    25. 80°

     

    27. 45°

     

    29. [latex]\frac{\pi }{3}[/latex]

     

    31. [latex]\frac{\pi }{3}[/latex]

     

    33. [latex]\frac{\pi }{8}[/latex]

     

    35. [latex]60°,[/latex] Quadrant IV,[latex]\,\text{sin}\left(300°\right)=-\frac{\sqrt{3}}{2},\mathrm{cos}\left(300°\right)=\frac{1}{2}[/latex]

     

    37. [latex]45°,[/latex] Quadrant II,[latex]\text{sin}\left(135°\right)=\frac{\sqrt{2}}{2},\mathrm{cos}\left(135°\right)=-\frac{\sqrt{2}}{2}[/latex]

     

    39. [latex]\,60°,[/latex] Quadrant II,[latex]\,\text{sin}\left(120°\right)=\frac{\sqrt{3}}{2},\mathrm{cos}\left(120°\right)=-\frac{1}{2}[/latex]

     

    41. [latex]30°,[/latex] Quadrant II,[latex]\,\text{sin}\left(150°\right)=\frac{1}{2},\mathrm{cos}\left(150°\right)=-\frac{\sqrt{3}}{2}[/latex]

     

    43. [latex]\frac{\pi }{6},[/latex] Quadrant III,[latex]\,\text{sin}\left(\frac{7\pi }{6}\right)=-\frac{1}{2},\mathrm{cos}\left(\frac{7\pi }{6}\right)=-\frac{\sqrt{3}}{2}[/latex]

     

    45. [latex]\frac{\pi }{4},[/latex] Quadrant II,[latex]\,\text{sin}\left(\frac{3\pi }{4}\right)=\frac{\sqrt{2}}{2},\mathrm{cos}\left(\frac{4\pi }{3}\right)=-\frac{\sqrt[]{2}}{2}[/latex]

     

    47. [latex]\frac{\pi }{3},[/latex] Quadrant II,[latex]\,\text{sin}\left(\frac{2\pi }{3}\right)=\frac{\sqrt{3}}{2},\mathrm{cos}\left(\frac{2\pi }{3}\right)=-\frac{1}{2}[/latex]

     

    49. [latex]\frac{\pi }{4},[/latex] Quadrant IV,[latex]\,\text{sin}\left(\frac{7\pi }{4}\right)=-\frac{\sqrt{2}}{2},\text{cos}\left(\frac{7\pi }{4}\right)=\frac{\sqrt{2}}{2}[/latex]

     

    51. [latex]\frac{\sqrt{77}}{9}[/latex]

     

    53. [latex]-\frac{\sqrt{15}}{4}[/latex]

     

    55. [latex]\left(-10, 10\sqrt{3}\right)[/latex]

     

    57. [latex]\left(–2.778,\text{ }15.757\right)[/latex]

     

    59. [latex]\left[–1,\text{ }1\right][/latex]

     

    61. [latex]\mathrm{sin}\left(t\right)=\frac{1}{2},\mathrm{cos}\left(t\right)=-\frac{\sqrt{3}}{2}[/latex]

     

    63. [latex]\mathrm{sin}\left(t\right)=-\frac{\sqrt{2}}{2},\mathrm{cos}\left(t\right)=-\frac{\sqrt{2}}{2}[/latex]

     

    65. [latex]\mathrm{sin}\left(t\right)=\frac{\sqrt{3}}{2},\mathrm{cos}\left(t\right)=-\frac{1}{2}[/latex]

     

    67. [latex]\mathrm{sin}\left(t\right)=-\frac{\sqrt{2}}{2},\mathrm{cos}\left(t\right)=\frac{\sqrt{2}}{2}[/latex]

     

    69. [latex]\mathrm{sin}\left(t\right)=0, \mathrm{cos}\left(t\right)=-1[/latex]

     

    71. [latex]\mathrm{sin}\left(t\right)=-0.596, \mathrm{cos}\left(t\right)=0.803[/latex]

     

    73. [latex]\mathrm{sin}\left(t\right)=\frac{1}{2},\mathrm{cos}\left(t\right)=\frac{\sqrt{3}}{2}[/latex]

     

    75. [latex]\mathrm{sin}\left(t\right)=-\frac{1}{2},\mathrm{cos}\left(t\right)=\frac{\sqrt{3}}{2}[/latex]

     

    77. [latex]\mathrm{sin}\left(t\right)=0.761,\mathrm{cos}\left(t\right)=-0.649[/latex]

     

    79. [latex]\mathrm{sin}\left(t\right)=1,\mathrm{cos}\left(t\right)=0[/latex]

     

    81. −0.1736

     

    83. 0.9511

     

    85. −0.7071

     

    87. −0.1392

     

    89. −0.7660

     

    91. [latex]\frac{\sqrt{2}}{4}[/latex]

     

    93. [latex]-\frac{\sqrt{6}}{4}[/latex]

     

    95. [latex]\frac{\sqrt{2}}{4}[/latex]

     

    97. [latex]\frac{\sqrt{2}}{4}[/latex]

     

    99. 0

     

    101. [latex]\left(0,–1\right)[/latex]

     

    103. 37.5 seconds, 97.5 seconds, 157.5 seconds, 217.5 seconds, 277.5 seconds, 337.5 seconds

     

    License

    Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

    Baylor University's Co-requisite Supplement for Calculus I Copyright © 2023 by Amy Graham Goodman is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

    Share This Book